


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | SYMBOLIC LOGIC AND THE ALGEBRA OF PROPOSITIONS-Functionally complete sets of operations |
|
|
|
Read More
Date: 5-1-2017
Date: 28-12-2016
Date: 28-12-2016
|
A set of operations is functionally complete provided every propositional function can be expressed entirely in terms of operations in the set. To exhibit a functionally complete set, we recall that every propositional function has a truth table. Further, every truth table corresponds to a unique expression in dis- junctive (or conjunctive) normal form, involving only the operations (+),(.) and ('). Hence the set {+,. , '} is functionally complete.
Since the proposition pq is equal to the proposition (p' + q')' by the law of De Morgan, it is possible to replace each occurrence of conjunction in any propositional function with an equivalent expression involving only (+) and ('). This shows that {+, '} is a functionally complete set of operations. Other functionally complete sets are {.,΄}and { →, '}.
It is possible to define a single operation which constitutes a functionally complete set. Suppose that we define p↓q by Table 1-1. This
TABLE 1-1
DEFINITION OF p↓q
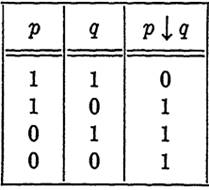
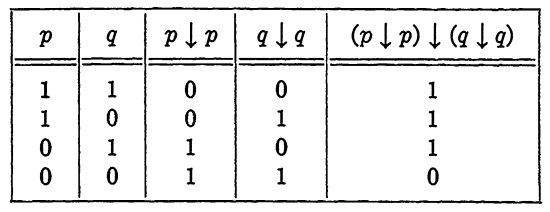
operation can be interpreted as "not both p and q." To see how this operation alone constitutes a functionally complete set, consider Table 1-2. From this table, we observe that p' = p ↓ p and p + q = (p↓p) I (q ↓q). But we have shown that every propositional function can be expressed in terms of (+) and ('). Each occurrence of (+) and (') may be replaced by the equivalent expression in terms of (↓), and henceevery propositional function can be written entirely in terms of the operation (↓). The operation (↓) is one of two operations known as Shefer stroke functions.
Table 1-2



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|