
Newton’s gravitational theory in quasi-field-theoretical form
 المؤلف:
Heino Falcke and Friedrich W Hehl
المؤلف:
Heino Falcke and Friedrich W Hehl
 المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
 الجزء والصفحة:
p 3
الجزء والصفحة:
p 3
 23-1-2017
23-1-2017
 2104
2104
Newton’s gravitational theory in quasi-field-theoretical form
The gravitational force of a pointlike mass m2 on a similar one of mass m1 is given by Newton's attraction law:
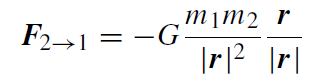 (1.1)
(1.1)
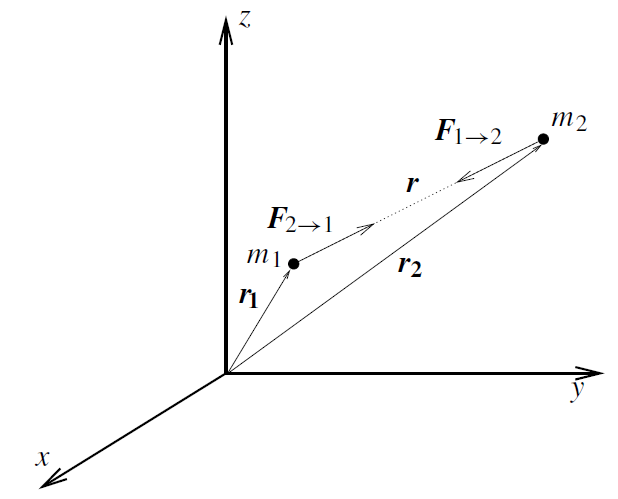
Figure 1.1. Two mass points m1 and m2 in three-dimensional space, Cartesian coordinates x, y, z.
where G is Newton's gravitational constant,
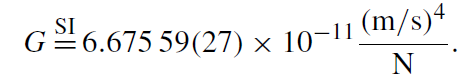
The vector r := r1 − r2 points from m2 to m1, see figure 1.1. According to actio = reactio (Newton's third law), we have F2→1 = −F1→2. Thus complete symmetry exists in the gravitational interaction of the two masses with each other. Let us now distinguish the mass m2 as a field-generating active gravitational mass and m1 as a (pointlike) passive test mass. Accordingly, we introduce a hypothetical gravitational field describing the force per unit mass (m2 → M,m1 → m):
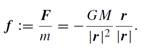 (1.2)
(1.2)
With this definition, the force acting on the test mass m is equal to the field strength × gravitational charge (mass) or FM→m = m f , in analogy to electrodynamics. The active gravitational mass M is thought to emanate a gravitational field which is always directed to the center of M and has the same magnitude on every sphere with M as center, see figure 1.2.
Let us now investigate the properties of the gravitational field (1.2). Obviously, there exists a potential
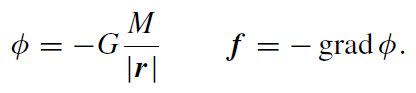 (1.3)
(1.3)
Accordingly, the gravitational field is curl free: curl f = 0.
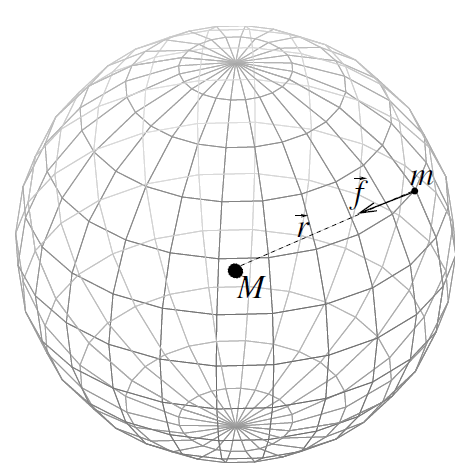
Figure 1.2. The ‘source’ M attracts the test mass m.
By assumption it is clear that the source of the gravitational field is the mass M. We find, indeed, that
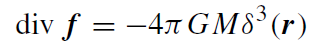 (1.4)
(1.4)
where δ3(r) is the three-dimensional (3D) delta-function. By means of the Laplace operator Δ := div grad, we infer, for the gravitational potential, that
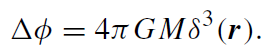 (1.5)
(1.5)
The term M δ3(r) may be viewed as the mass density of a point mass. Equation (1.5) is a second-order linear partial differential equation for φ. Thus the gravitational potential generated by several point masses is simply the linear superposition of the respective single potentials. Hence we can generalize the Poisson equation (1.5) straightforwardly to a continuous matter distribution ρ(r):
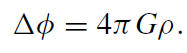 (1.6)
(1.6)
This equation interrelates the source ρ of the gravitational field with the gravitational potential φ and thus completes the quasi-field-theoretical description of Newton's gravitational theory.
We speak here of quasi-field-theoretical because the field φ as such represents a convenient concept. However, it has no dynamical properties, no genuine degrees of freedom. The Newtonian gravitational theory is an action at a distance theory. When we remove the source, the field vanishes instantaneously. Newton himself was very unhappy about this consequence. Therefore he emphasized the preliminary and purely descriptive character of his theory. But before we liberate the gravitational field from this constraint by equipping it with its own degrees of freedom within the framework of general relativity theory, we turn to some properties of the Newtonian theory.
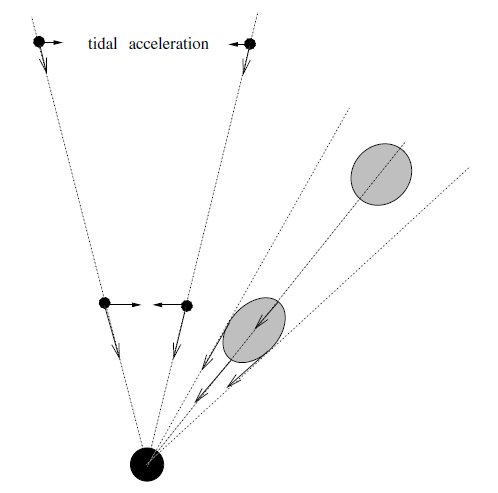
Figure 1.3. Tidal forces in a spherically symmetric gravitational field.
A very peculiar fact characteristic to the gravitational field is that the acceleration of a freely falling test body does not depend on the mass of this body but only on its position within the gravitational field. This comes about because of the equality (in suitable units) of the gravitational and inertial mass: inertial
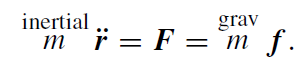 (1.7)
(1.7)
This equality has been well tested since Galileo's time by means of pendulum and other experiments with an ever increasing accuracy.
In order to allow for a more detailed description of the structure of a gravitational field, we introduce the concept of a tidal force. This can be best illustrated by means of figure 1.3. In a spherically symmetric gravitational field, for example, two test masses will fall radially towards the center and thereby get closer and closer. Similarly, a spherical drop of water is deformed to an ellipsoidal shape because the gravitational force at its bottom is bigger than at its top, which is at a greater distance from the source. If the distance between two freely falling test masses is relatively small, we can derive an explicit expression for their relative acceleration by means of a Taylor expansion. Consider two mass points with position vectors r and r +δr, with |δr| << 1. Then the relative acceleration reads:
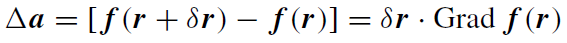 (1.8)
(1.8)
where Grad denotes the vector gradient. We may rewrite this accordingly (the sign is conventional, ∂/∂xa =: ∂α, x1 = x, x2 = y, x3 = z):
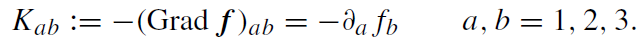
We call Kab the tidal force matrix. The vanishing curl of the gravitational field is equivalent to the symmetry Kab = Kba. Furthermore, Kab = ∂a∂bφ. Thus, the Poisson equation becomes
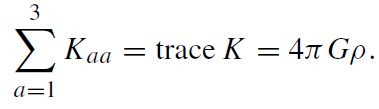 (1.9)
(1.9)
Accordingly, in vacuum Kab is trace free.
Let us now investigate the gravitational potential of a homogeneous star with constant mass density ρּ and total mass Mּ = (4/3)π R3ּρּ. For our sun, the radius is Rּ = 6.9598× 108 m and the total mass is M = 1.989 × 1030 kg.
Outside the sun (in the idealized picture we are using here), we have a vacuum. Accordingly, ρ(r) = 0 for |r| > Rּ. Then the Poisson equation reduces to the Laplace equation
 (1.10)
(1.10)
In 3D polar coordinates, the r-dependent part of the Laplacian has the form (1/r 2)∂r (r 2∂r ). Thus (1.10) has the solution
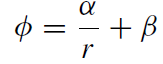 (1.11)
(1.11)
where α and β are integration constants. Requiring that the potential tends to zero as r goes to infinity, we get β = 0. The integration constant α will be determined from the requirement that the force should change smoothly as we cross the star's surface, i.e. the interior and exterior potentials and their first derivatives have to be matched continuously at r = Rּ.
Inside the star we have to solve
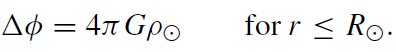 (1.12)
(1.12)
We find
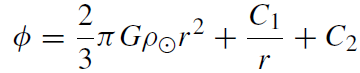 (1.13)
(1.13)
with integration constants C1 and C2. We demand that the potential in the center r = 0 has a finite value, say φ0. This requires C1=0. Thus
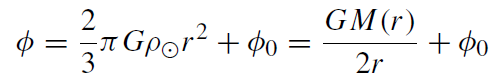 (1.14)
(1.14)
where we have introduced the mass function M(r ) = (4/3)πr 3ρּ which measures the total mass inside a sphere of radius r .
Continuous matching of φ and its first derivatives at r = Rּ finally yields:
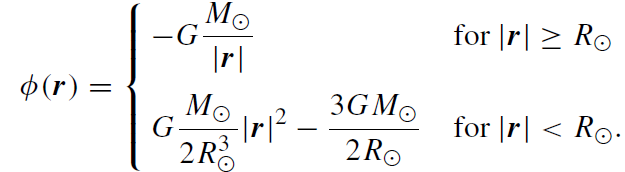 (1.15)
(1.15)
The slope (first derivative) and the curvature (second derivative) of this curve represent the magnitudes of the gravitational and the tidal forces, respectively.
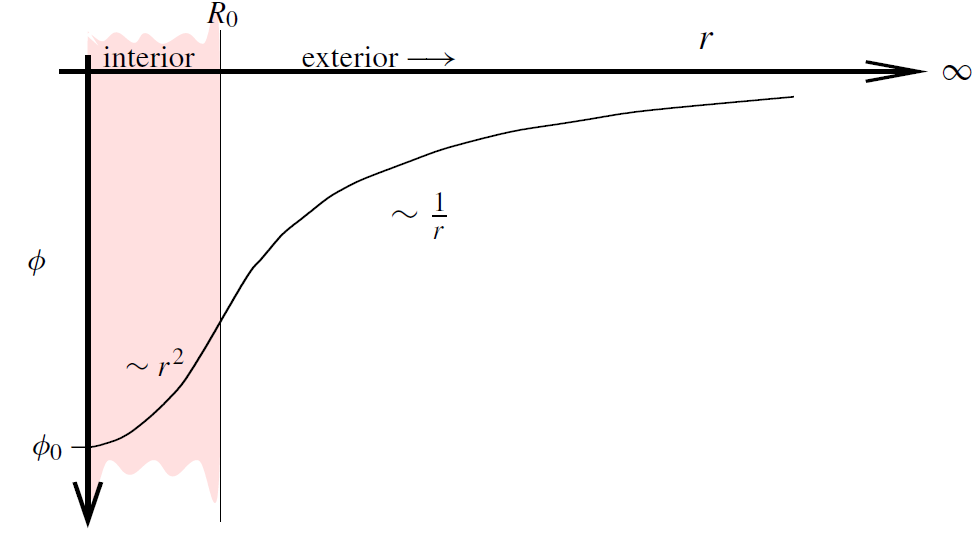
Figure 1.4. Newtonian potential of a homogeneous star.
Gravity exists in all bodies universally and is proportional to the quantity of matter in each . . . If two globes gravitate towards each other, and their matter is homogeneous on all sides in regions that are equally distant from their centers, then the weight of either globe towards the other will be inversely as the square of the distance between the centers.
Isaac Newton (1687)
 الاكثر قراءة في مواضيع عامة في النظرية النسبية
الاكثر قراءة في مواضيع عامة في النظرية النسبية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


