

علم الكيمياء

تاريخ الكيمياء والعلماء المشاهير

التحاضير والتجارب الكيميائية

المخاطر والوقاية في الكيمياء

اخرى

مقالات متنوعة في علم الكيمياء

كيمياء عامة


الكيمياء التحليلية

مواضيع عامة في الكيمياء التحليلية

التحليل النوعي والكمي

التحليل الآلي (الطيفي)

طرق الفصل والتنقية


الكيمياء الحياتية

مواضيع عامة في الكيمياء الحياتية

الكاربوهيدرات

الاحماض الامينية والبروتينات

الانزيمات

الدهون

الاحماض النووية

الفيتامينات والمرافقات الانزيمية

الهرمونات


الكيمياء العضوية

مواضيع عامة في الكيمياء العضوية

الهايدروكاربونات

المركبات الوسطية وميكانيكيات التفاعلات العضوية

التشخيص العضوي

تجارب وتفاعلات في الكيمياء العضوية


الكيمياء الفيزيائية

مواضيع عامة في الكيمياء الفيزيائية

الكيمياء الحرارية

حركية التفاعلات الكيميائية

الكيمياء الكهربائية


الكيمياء اللاعضوية

مواضيع عامة في الكيمياء اللاعضوية

الجدول الدوري وخواص العناصر

نظريات التآصر الكيميائي

كيمياء العناصر الانتقالية ومركباتها المعقدة


مواضيع اخرى في الكيمياء

كيمياء النانو

الكيمياء السريرية

الكيمياء الطبية والدوائية

كيمياء الاغذية والنواتج الطبيعية

الكيمياء الجنائية


الكيمياء الصناعية

البترو كيمياويات

الكيمياء الخضراء

كيمياء البيئة

كيمياء البوليمرات

مواضيع عامة في الكيمياء الصناعية

الكيمياء الاشعاعية والنووية
Acetic acid and other weak acids
المؤلف:
John T. Moore, EdD
المصدر:
Chemistry Essentials For Dummies
الجزء والصفحة:
p 150
26-1-2017
2441
Acetic acid and other weak acids
Suppose that you dissolve acetic acid (CH3COOH) in water. It reacts with the water molecules, donating a proton and forming hydronium ions. It also establishes equilibrium, where you have a significant amount of unionized acetic acid. The acetic acid reaction with water looks like this:
CH3COOH(l) + H2O(l) ↔ CH3COO– + H3O+
The amount of hydronium ion that you get in solutions of acids that don’t ionize completely is much less than it is with a strong acid. Acids that only partially ionize are called weak acids. In the case of acetic acid, about 5 percent ionizes, and 95 percent remains in the molecular form.
Calculating the hydronium ion concentration in weak acid solutions isn’t as straightforward as it is in strong solutions, because not all the weak acid that dissolves initially has ionized. To calculate the hydronium ion concentration, you must use the equilibrium constant expression for the weak
acid.
For weak acid solutions, you use a modified equilibrium constant expression called the Ka — the acid ionization constant. One way to distinguish between strong and weak acids is to look for an acid ionization constant (Ka) value. If the acid has a Ka value, then it’s weak. Take a look at the generalized ionization of some weak acid HA:
HA + H2O ↔ A– + H3O+
The Ka expression for this weak acid is
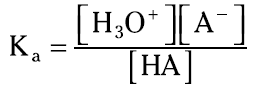
Note that the [HA] represents the molar concentration of HA at equilibrium, not initially. Also, note that the concentration of water doesn’t appear in the Ka expression, because there’s so much that it actually becomes a constant incorporated into the Ka expression.
Now go back to that acetic acid equilibrium. The Ka for acetic acid is 1.8 × 10–5. The Ka expression for the acetic acid ionization is
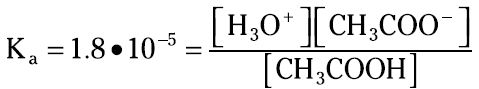
You can use this Ka when calculating the hydronium ion concentration in, say, a 2.0 M solution of acetic acid. You know that the initial concentration of acetic acid is 2.0 M. You know that a little bit has ionized, forming a little hydronium ion and acetate ion. You also can see from the balanced reaction that for every hydronium ion that’s formed, an acetate ion is also formed — so their concentrations are the same. You can represent the amount of [H3O+] and [CH3COO–] as x, so
[H3O+] = [CH3COO–] = x
To produce the x amount of hydronium and acetate ion, the same amount of ionizing acetic acid is required. So you can represent the amount of acetic acid remaining at equilibrium as the amount you started with, 2.0 M, minus the amount that ionizes, x:
[CH3COOH] = 2.0 – x
For the vast majority of situations, you can say that x is very small in comparison to the initial concentration of the weak acid. So you can say that 2.0 – x is approximately equal to 2.0.
This means that you can often approximate the equilibrium concentration of the weak acid with its initial concentration. The equilibrium constant expression now looks like this:
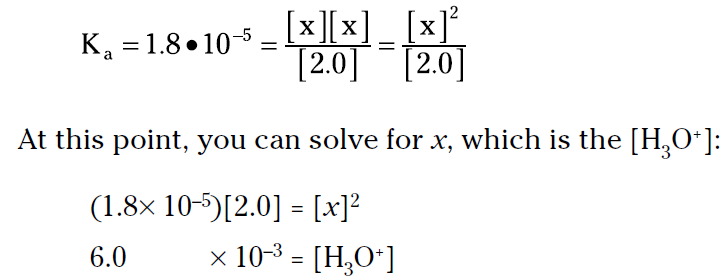
 الاكثر قراءة في مقالات متنوعة في علم الكيمياء
الاكثر قراءة في مقالات متنوعة في علم الكيمياء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















