
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Primordial black holes
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 221
26-1-2017
2263
Primordial black holes
Can the previously discussed quantum effects of black holes be observed? As has already been mentioned, black holes formed by stellar collapse are much too heavy to exhibit quantum behaviour. To form smaller black holes one needs higher densities which can only occur under the extreme situations of the early Universe. Such primordial black holes can originate in the radiation-dominated phase during which no stars or other objects can be formed.
Consider for simplicity a spherically symmetric region with radius R and density ρ = ρc + δρ embedded in a flat Universe with the critical density ρc, cf Carr (1985). For spherical symmetry the inner region is not affected by matter in the surrounding part of the Universe, so it will behave like a closed Friedmann Universe (since its density is overcritical), i.e. the expansion of this region will come to a halt at some stage, followed by a collapse. In order to reach a complete collapse, the (absolute value of the) potential energy, V , at the time of maximal expansion has to exceed the inner energy, U, given by the pressure p, that is,
 (1.1)
(1.1)
If the equation of state reads as p = wR (w = 1/3 for radiation dominance), this gives
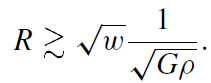 (1.2)
(1.2)
The lower bound for R is thus just given by the Jeans length. An upper bound also exists. The reason is that R must be smaller than the curvature radius (given by 1/√Gρ) of the over dense region at the moment of collapse. Otherwise the region would contain a compact three-sphere which is topologically disconnected from the rest of the Universe. This case would not then lead to a black hole within our Universe. Using ρ ∼ ρc ∼ H2/G, where H denotes the Hubble parameter of the background flat Universe, one has the condition
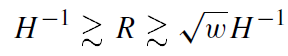 (1.3)
(1.3)
evaluated at the time of collapse, for the formation of a black hole. This relation can also be rewritten as a condition referring to any initial time of interest (Carr 1985). In particular, one is often interested in the time where the fluctuation enters the horizon in the radiation-dominated Universe. This is illustrated in figure 1.1, where the presence of a possible inflationary phase at earlier times is also shown.
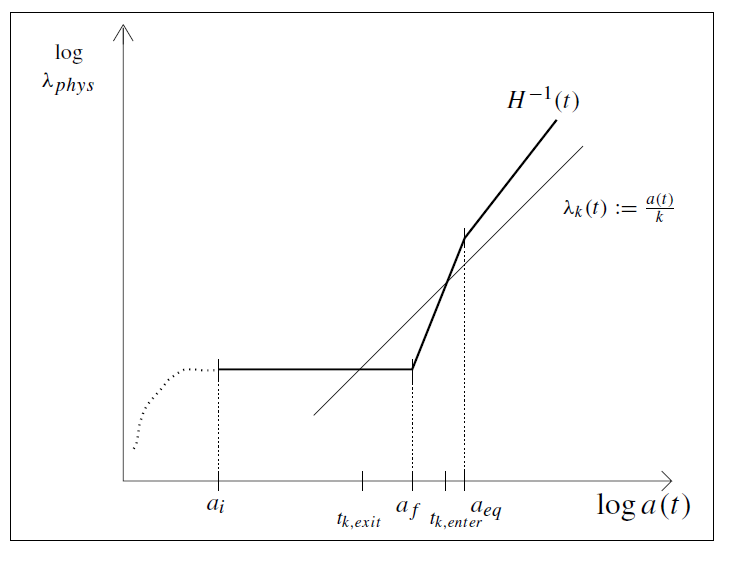
Figure 1.1. Time development of a physical scale λ(t) and the Hubble horizon H−1(t). During an inflationary phase H−1(t ) remains approximately constant. After the end of inflation (a f ) the horizon H−1(t ) increases faster than any scale. Therefore λk enters the horizon again at tk,enter in the radiation- (or matter-) dominated phase.
At horizon entry one gets, denoting δ ≡ δρ/ρc,
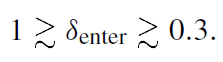 (1.4)
(1.4)
This is, however, only a rough estimate. Numerical calculations give instead the bigger value of δmin ≈ 0.7 (Niemeyer and Jedamzik 1999). Taking from (1.3) R ≈ √wH−1, one gets for the initial mass of a primordial black hole (PBH)
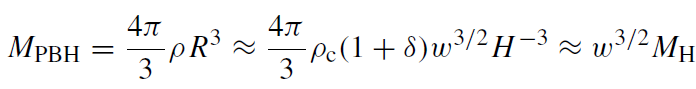 (1.5)
(1.5)
where MH ≡ (4π/3)ρcH−3 denotes the mass inside the horizon. Since MPBH is of the order of this horizon mass, a collapsing region will form a black hole practically immediately after horizon entry. Using the relation MH = t/G, valid for a radiation-dominated Universe, one gets from (1.5) the quantitative estimate
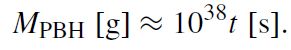 (1.6)
(1.6)
This means that one can create Planck-mass black holes at the Planck time, and PBHs with MPBH ≈ 5 × 1014 g at t ≈ 5 × 10−24 s. The latter value is important since, black holes with masses smaller than MPBH ≈ 5 × 1014 g have by now evaporated due to Hawking radiation. PBHs with bigger mass are still present today. At t ≈ 10−5 s, one can create a solar mass black hole and at t ≈ 10 s (the time of nucleosynthesis) one could form a PBH with the mass of the Galactic black hole. The initial mass can increase by means of accretion, but it turns out that this is negligible under most circumstances (Carr 1985).
In the presence of an inflationary phase in the early Universe, all PBHs produced before the end of inflation are diluted away. This gives the bound
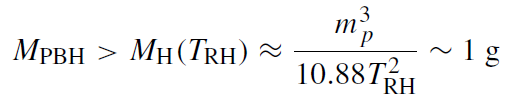 (1.7)
(1.7)
if for the reheating temperature TRH a value of 1016 GeV is chosen.
According to the numerical calculations by Niemeyer and Jedamzik (1999), there exists a whole spectrum of initial masses,
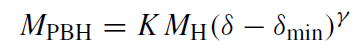 (1.8)
(1.8)
a relation that is reminiscent of the theory of critical phenomena. This may change some of the quantitative conclusions.
To calculate the production rate of PBHs, one needs an initial spectrum of fluctuations. This is usually taken to be of a Gaussian form, as predicted by most inflationary models (cf Liddle and Lyth 2000). Therefore, there always exists a non-vanishing probability that the density contrast is high enough to form a black hole, even if the maximum of the Gaussian corresponds to a small value. One can then calculate the mass ratio (compared to the total mass) of regions which will develop into PBHs with mass MPBH > M, see, e.g., Bringmann et al (2001) for details. This mass ratio, given by
 (1.9)
(1.9)
where ρr is the radiation density, is then compared with observation. This, in turn, gives a constraint on the theoretically calculated initial spectrum. Table 1.1 presents various observational constraints on α (see Green and Liddle 1997). The corresponding maximal value for each α is shown for the various constraints in figure 1.1.
Constraints arise either from Hawking radiation or from the gravitational contribution of PBHs to the present Universe (last entry). PBHs with initial mass of about 5 × 1014 g evaporate ‘today’. (They release about 1030 erg in the last second.) From observations of the γ -ray background one can find the constraint given in table 1.1 which corresponds to an upper limit of about 104 PBHs per cubic parsec or ΩPBH,0 < 10−8. One can also try to observe directly the final evaporation event of a single PBH. This gives an upper limit of about 4.4 × 105 events per cubic parsec per year.
Given these observational constraints, one can then calculate the ensuing constraints on the primordial spectrum. The gravitational constraint ΩPBH,0 < 1 gives surprisingly strong restrictions (cf Bringmann et al 2001). For a scale free spectrum of the form ∝ kn, as is usually discussed for inflationary models,
Table 1.1. Constraints on the mas fraction α(M) := ρPBH,M/ρr ≈ ΩPBH,M of primordial black holes at their time of formation (Green and Liddle 1997).

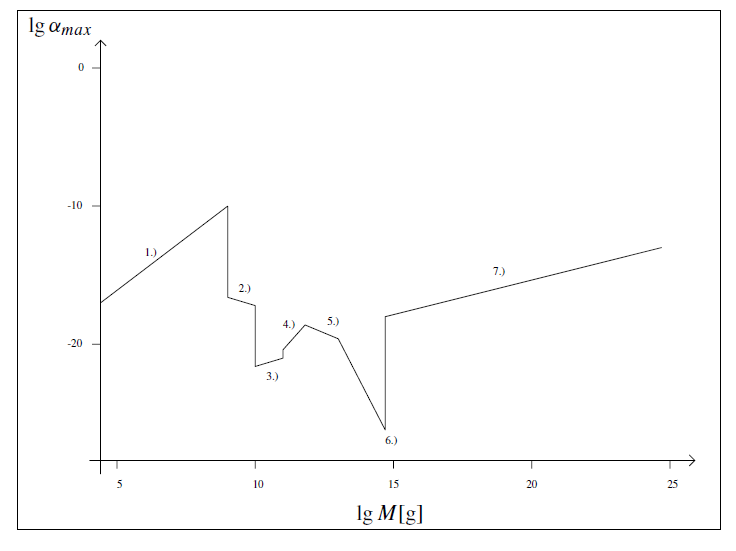
Figure 1.2. Strongest constraints on the initial PBH mass fraction. The numbers correspond to the various entries in table 1.1.
one finds restrictions on n that are comparable to the limits obtained by large scale observations (the anisotropy spectrum of the cosmic microwave background radiation). Since these restrictions come from observational constraints referring to much smaller scales, they constitute an important complementary test.
The question as to whether PBHs really exist in nature has thus not yet been settled. Their presence would be of an importance that could hardly be overestimated. They would give the unique opportunity to study the quantum effects of black holes and could yield the crucial key for the construction of a final theory of quantum gravity.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















