
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Evolution of the scalar massless field around a non-rotating black hole
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 153
2-2-2017
2133
Evolution of the scalar massless field around a non-rotating black hole
1.1 Retarded Green’s function
Time evolution of the scalar massless field around a non-rotating black hole for given initial data and source jℓ can be easily obtained by using a retarded Green’s function Gret. The retarded Green's function is a solution of the equation
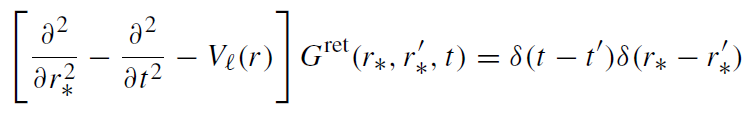 (1.1)
(1.1)
which is singled out by the condition G(r∗, r'∗ , t – t') = 0 for t < t'.
The integral transform, reducing the problem to an ordinary differential equation,
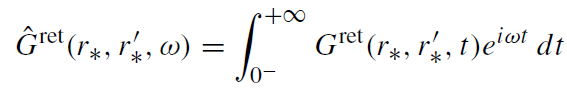 (1.2)
(1.2)
is well defined as long as Imω ≥ 0. In fact, Ĝret(r∗, r'∗,ω) is a holomorphic function of ω = ω0 + iω1 for ω1 > 0. By a change s = -iω, one can show that this integral transform is nothing but the usual Laplace transform. By making the inverse Laplace transformation one obtains
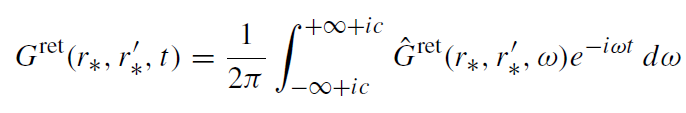 (1.3)
(1.3)
where c is some positive number (this ensures convergence of the integral).
1.2 Green’s function representation
The integral transform of the retarded Green's function obeys the equation
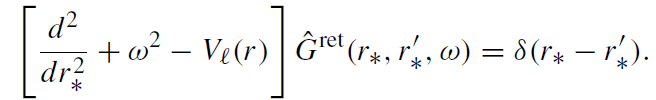 (1.4)
(1.4)
Since the retarded Green's function Gret(x, x') vanishes when a point x' lies to the past of x, in its decomposition there must be no waves which emerge from  − and H−. Thus Ĝret(r∗, r'∗,ω) can be written as
− and H−. Thus Ĝret(r∗, r'∗,ω) can be written as
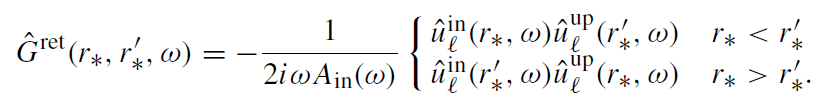 (1.5)
(1.5)
The factor containing Ain is the Wronskian.
1.3 Analytical properties
In order to infer the behavior of the Green's function in different time intervals it is convenient to deform the contour of integration in the complex ω-plane. For this purpose we need to know the analytic properties of ûinℓ and ûupℓ, not only in the upper half-plane where they are a holomorphic functions of ω, but also in the lower half-plane. A detailed analysis of this problem can be found in [19]. Here we just describe the most important results.
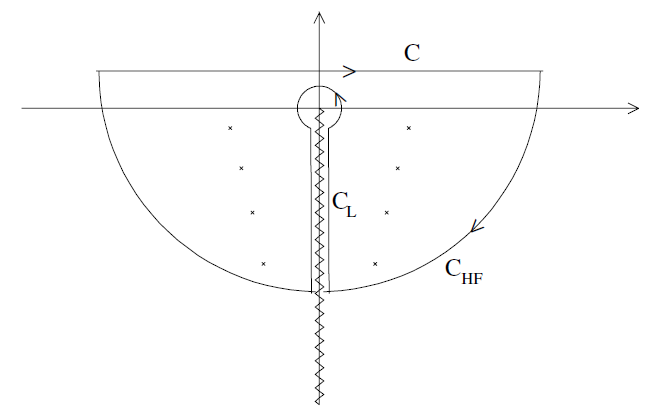
Figure 1.1. Integration contours in the complex ω-plane. The crosses represent the first few quasinormal modes. The necessary branch cut is taken along the negative imaginary axis.
The analysis shows that the Wronskian W(IN,UP) = 2iωAin(ω) has isolated zeros there. This leads to poles of the Green's function Ĝret(r∗, r'∗,ω). These singularities correspond directly to the so called quasinormal modes of the black hole. It is straightforward to show that the poles are symmetrically distributed with respect to the imaginary ω-axis; if ωn corresponds to Ain = 0, then -ϖn must also do so (see figure 1.1).
In the upper half of the complex ω-plane, the solutions, which are bound at either end, must behave like
 (1.6)
(1.6)
Their analytical continuations into the lower half-plane will show the same behavior. Hence, the Green's function always satisfies ‘future outgoing’ conditions. This Green's function propagates waves emitted by the source to H+ and  +. It is therefore clear that the solutions corresponding to the quasinormal modes are regular both at H+ and
+. It is therefore clear that the solutions corresponding to the quasinormal modes are regular both at H+ and  +. But it also follows that they will diverge at H −and
+. But it also follows that they will diverge at H −and  −.
−.
Careful analysis shows that it is necessary to introduce a branch cut in order to make ûupℓ a single-valued function [20]. This cut is usually placed along the negative imaginary axis, as in figure 1.1.
Given this information, the radiation produced in response to a perturbation of the black hole can be divided into three components, in accordance with the contributions from different parts of the deformed contour in the lower half of the ω-plane:
(i) radiation emitted directly by the source,
(ii) exponentially damped quasinormal-mode oscillations (contribution of the poles of the Green's function) and
(iii) a power-law tail (contribution of the branch cut integral).
1.4 Quasinormal modes
Scattering resonances (which are the quantum analogues to quasinormal modes) arise for energies close to the top of a potential barrier. In the black hole case, this immediately leads to the approximation
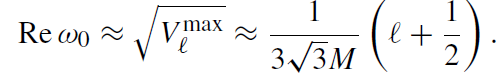 (1.7)
(1.7)
This approximation for the fundamental mode is poor for low ℓ (the error is something like 30% for ℓ = 2) but it rapidly gets accurate as ℓ increases.
For the imaginary part of the frequency the lifetime of the resonance the curvature of the potential contains the relevant information [21]. One finds that
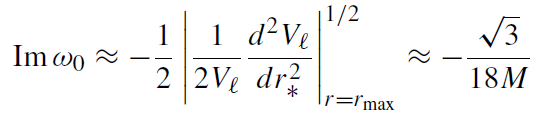 (1.8)
(1.8)
which is accurate to within 10% for the fundamental mode.
Interestingly, similar approximations follow from a different approach. Consider a congruence of null rays circling the black hole in the unstable photon orbit at r = 3M. The fundamental mode frequency then follows if the beam contains ℓ cycles [24]. The damping rate of the mode can be inferred from the decay rate of the congruence if the null orbit is slightly perturbed [25].
It is interesting to compare a black hole to other resonant systems in nature. If we define a quality factor in analogy with the standard harmonic oscillator,
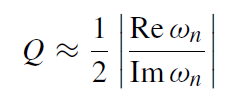 (1.9)
(1.9)
the quasinormal-mode approximations given here lead to Q ≈ ℓ. This should be compared to the typical value for an atom: Q ∼ 106. The Schwarzschild black hole is thus a very poor oscillator.
1.5 Late-time behavior
The power-law tail is associated with the branch-cut integral along the negative imaginary axis in the complex ω-plane. The main contribution gives the |ωM| << 1 part of that integral. A branch-cut contribution to the Green's function is [19,20]
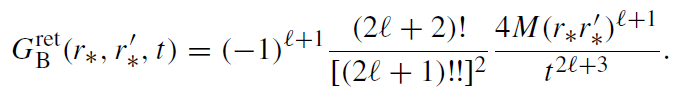 (1.10)
(1.10)
This result implies that if the source of radiation falls down beyond the potential barrier the damping of its radiation that is seen by a distant observer is not purely exponential. The late-time behavior of the field is
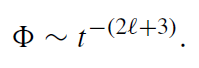 (1.11)
(1.11)
This power-law behavior is connected with the scattering of emitted radiation by the ‘tail’ of the potential barrier (by the spacetime curvature).
Price [26] found that backscattering by the asymptotic ‘tail’ of the potential gives rise to a power-law fall-off at late times. Price put his conclusions in the following succinct form: ‘Anything that can be radiated will be radiated.’ Consequently, a black hole gets rid of all bumps after it is formed by a non-spherical collapsing star.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















