


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-1-2022
Date: 14-2-2017
Date: 27-12-2021
|
In this section we shall encounter several ways of obtaining sets from previously given ones.
Definition 1. 1. Let A and B be given sets; then
1. The intersection A ∩ B of A and B is defined by
A ∩ B = {x : x ∈ A and x ∈ B}
If A ∩ B = ∅, then A and B are called disjoint.
2. The union A ∪ B of A and B is defined by
A ∪ B = {x : x ∈ A or x ∈ B}.
3. The set difference A B of A and B is the set
A B = {x : x ∈ A and x ∉ B}.
A B is also called the relative complement of B with respect to A.
If U is a given universal set, then U A is just called the complement of A, written as −A.
Observe that A ∩ B is the set of those objects which are simultaneously in both A and B, while A ∪ B is the set of those objects which are in A or in B or in both of them; observe carefully that we do not interpret “or” as exclusive; in our terminology, “or” always means “one, or the other, or both”.
Example 1. 1. Let
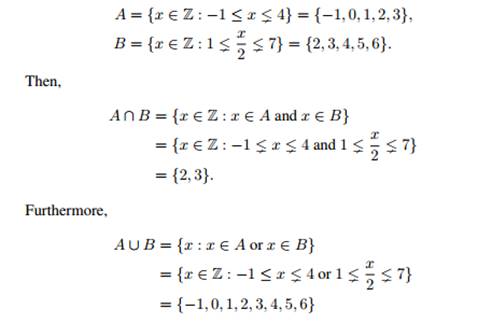
2. Let g1 and g2 be two non–parallel lines in the plane. Then, their intersection g1 ∩ g2 is just the point where the two lines meet. Their union g1 ∪ g2 is the set of all points which are on g1 or on g2 (or on both lines).
3. Let R be the set of all station wagons in Iceland at a given time, and let S be the set of all white cars in Iceland. Then S ∩ T is the set of all white station wagons in Iceland, and S ∪ T is the set of all those cars in Iceland which are a station wagon or which are white or both.
4. Let U = N, and A = {x ∈ N : x is prime}. Then −A is the set of all those natural numbers which are less than 2 or have at least three divisors.
5. Let U = N, and A be the set of all even natural numbers. Then −A is the set of all odd natural numbers.
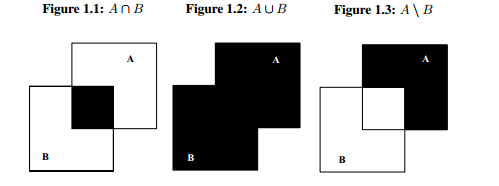
A convenient pictorial representation of the operations defined above are the Venn diagrams, shown in Fig. 1.1 – 1.3 on the following page: The shaded area represents
the result of the respective operation.
Lemma 1. 1. Let A ⊆ U; then
A ∩ A = A, A ∪ A = A.
2. A ∩ ∅ = ∅, A ∪ ∅ = A.
3. A ∩ U = A, A ∪ U = U.
4. A ∩ −A = ∅, A ∪ −A = U.
Proof. We shall only show 1. and 2.; the rest is left as an exercise.
1. A ∩ A = {x ∈ U : x ∈ A and x ∈ A} = {x ∈ U : x ∈ A} = A.
A ∪ A = {x : x ∈ A or x ∈ A} = {x : x ∈ A} = A.
2. A ∩ ∅ = {x : x ∈ A and x ∈ ∅}; since ∅ has no elements, the right hand side (and thus the left hand side) of the equation is the empty set.
A ∪ ∅ = {x : x ∈ A or x ∈ ∅}; again, since ∅ has no elements, we do not “add” anything to A, hence, A ∪ ∅ = A.
Lemma 1. 2. If A and B are sets, then A ∩ B = B ∩ A, and A ∪ B = B ∪ A.
This is called the Law of Commutativity for ∩ and ∪.
Proof. We only prove the first part; the second part is similar:
A ∩ B = {x : x ∈ A and x ∈ B} = {x : x ∈ B and x ∈ A} = B ∩ A.
Since we have defined the operations ∩ and ∪ only for two sets, the expressions A ∩ B ∩ C and A ∪ B ∪ C do not make sense. However, if we write (A ∩ B) ∩ C and (A ∪ B)∪ C, then this instruct us first to find the intersection (union) of A and B, and then the intersection (union) of A ∩ B (A ∪ B) with C. On the other hand, we could also have interpreted the line A ∩ (B ∩ C) and A ∪ (B ∪ C), which tells us first to find the intersection (union) of B and C, and then proceed to A. The following Lemma shows that it does not matter what we do first - the result is the same.
Lemma 1. 3. If A,B, C are sets, then
1. (A ∩ B) ∩ C = A ∩ (B ∩ C)
2. (A ∪ B) ∪ C = A ∪ (B ∪ C)
This is called the Law of Associativity for ∩ and ∪.
Proof. We only prove 1. We have to show both inclusions, i.e If x ∈ (A ∩ B) ∩ C, then x ∈ A∩(B ∩C) and vice versa. “⊆”: Let x ∈ (A∩B)∩C; then, x ∈ A∩B and x ∈ C; since x is an element of A ∩ B, we obtain that x ∈ A and x ∈ B. Thus we have x ∈ A and x ∈ B and x ∈ C, which implies x ∈ A ∩ (B ∩ C).
The previous Lemma enables us to give a meaningful interpretation to expressions like A∩B∩C or A∪B∪C, e.g A∪B∪C = {x : x ∈ A or x ∈ B or x ∈ C}, and we shall omit the brackets where no confusion can arise. The law of associativity also allows us to consider more than three sets by grouping the sets in a convenient way.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|