
Sets-De Morgan Rules, Distributivity, Tables
 المؤلف:
Ivo Düntsch and Günther Gediga
المؤلف:
Ivo Düntsch and Günther Gediga
 المصدر:
Sets, Relations, Functions
المصدر:
Sets, Relations, Functions
 الجزء والصفحة:
17-19
الجزء والصفحة:
17-19
 14-2-2017
14-2-2017
 2227
2227
In the sequel, let U be a universal set, of which all other mentioned sets are subsets.
Our first Theorem in this section exhibits a connection between intersection, union, and complementation:
Theorem 1. 1. For all sets A,B
−(A ∪ B) = −A ∪ −B, −(A ∩ B) = −A ∪ −B
These are the Rules of De Morgan.
Proof. We only show the first part and leave the second as an exercise. “⊆”: Let x ∈ −(A ∪ B); then x is not in the union of A and B, hence, x is neither in A nor in B. Since x is not in A, we have x ∈ −A, and since x is not in B, we have x ∈ −B. Thus, x ∈ −A and x ∈ −B which implies that x ∈ −A ∩ −B.
“⊇′′: Conversely, let x ∈ −A ∩ −B; then x is not in A and x is not in B. Hence, x is not an element of A or B, i.e. x ∈ −(A ∪ B).
Even though the proofs of set equations are simple, they can be quite tedious, and we shall introduce a new tool for tackling problems of this sort.
If A and B are sets, then for an arbitrary element x of our universe of discourse U there are four possibilities:
x ∈ A and x ∈ B, x ∈ A and x ∉B x ∉A and x ∈ B, x ∉A and x ∉B.
For every one of these cases let us consider if x is in the intersection of A and B:
If x ∈ A and x ∈ B, then x ∈ A ∩ B. In all three other cases, we have x ∉A ∩ B.
This observation can be put in the form of a table which looks like this:
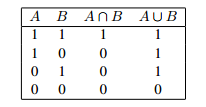
Here, an entry 1 means that x is in the set pointed to by the column head, and 0 tells us that it is not.
Regarding complementation, we have the following table:
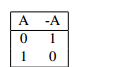
With these three tables we can find the table for every set which is formed from A and B by the operations ∩, ∪, and −. Let us look at the table for the first De Morgan rule:
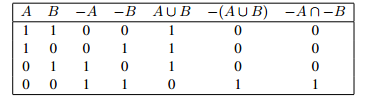
Observe that the right columns of the table have the same entries of in the corresponding places. This tells us that the two sets are equal.
Theorem 1. 2. For all sets A,B
A ∪ (A ∩ B) = A, A ∩ (A ∪ B) = A.
These are the absorption laws.
Proof. We shall only prove the first equation, and use a table:
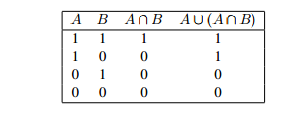
This proves our claim.
The method of tables can also be used with more than just two sets; then, of course, the number of possibilities increases, e.g. if we have sets A,B, C, then there are eight possibilities for an arbitrary x ∈ U, and if we have A,B,C, D then there are already sixteen. In general, if there are n sets, then a column in a table for each of these n sets will have 2n entries.
Our final Theorem in this section reveals the interplay between ∩ and ∪:
Theorem 1. 3. For all sets A,B, C,
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C), A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
These are the distributive Laws for ∩ and ∪.
 الاكثر قراءة في نظرية المجموعات
الاكثر قراءة في نظرية المجموعات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


