


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-2-2017
Date: 30-12-2021
Date: 12-1-2022
|
Definition 1.1. Let f : A → B be a function.
1. f is called onto or surjective if codom f = ran f. If f is surjective, we sometimes indicate this by writing f : A ։ B.
2. f is called one–one or injective if for all x, y ∈ A, f(x) = f(y) implies x = y. If f is injective, we sometimes indicate this by writing f : A → B.
3. f is called bijective if f is onto and one-one.
Thus, f is onto if, in the pictorial representation, at least one arrow arrives at every element of the codomain; in other words, for every y ∈ codom f there exists at least one element x of dom f with f(x) = y. If f is one–one, then at most one arrow arrives at every element of codom f. If f is bijective, then exactly one arrow arrives at every element of codom f, see Figure 1.1.
Figure 1.1: Types of functions
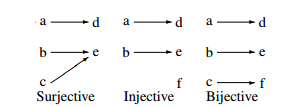
Example 1.1.
f is one–one: We have to show that for all x,y ∈ R,f(x) = f(y) implies x = y. So let f(x) = f(y); by definition of f, f(x) = 2x and f(y) = 2y.
Since f(x) = f(y), the definition of f tells us that 2x = 2y, which implies x = y.
f is onto: For every real number y we have to find a real number x such that f(x) = y, which, by our definition of f is the same as 2x = y. Solving this equation for x gives us x =y/2; so, f(y/2) = y.
Since f is one–one and onto, it is bijective.
2. f : R → R, f(x) = x2:
f is not one–one: To show that an object does not have a certain property, it is enough to exhibit one counterexample, So, to show that f is not one–one we have to find two different real numbers x and y such that f(x) = f(y).
This is easily done by choosing x = 1 and y = −1.
f is not onto: Again, we have to find just one counterexample. If e.g. y = −1, then for no real number x we have f(x) = y, since the square of a real number is never negative.
3. Let R+ be the set of positive real numbers and define f : R → R+ by f(x) = x2.
Observe that we have only changed the codomain of the previous example. The function still is not one–one, but now it is onto, since every positive real number is a square.
4. Let f : R+ → R be defined by f(x) = x2.
We have only changed the domain of f from Example 2. This function is not onto – the codomain is still all of R, and negative numbers still cannot be squares of real numbers.
But our new f is one–one, since every real number has at most one positive root.
These examples tell us that the properties of being one–one or onto depend not only on the rule of assignment, but also on the domain and the codomain of the function. In fact, by changing the codomain of a function, we can always obtain a surjective function with the same domain and the same rule of assignment:
Lemma 1.1. Let f : A → B be a function; then g : A → ran f defined by g(x) = f(x) for all x ∈ A is onto.
Proof. Since dom f = dom g, and g(x) = f(x) for all x ∈ A, g is a function. To show that g is onto, let y ∈ codom g. By our definition of g, codom g = ran f; thus there is an x ∈ A = dom f such that f(x) = y. Now, since dom f = dom g we have x ∈ dom g; furthermore, since f(x) = g(x), we obtain g(x) = y. This shows that g is onto.
Each function f : A → B can be written as a composition f = h ◦ g of functions, where g is surjective, and h is injective. This is an important Theorem which is used in many algebraic contexts. To prepare for a proof, we need
Definition 1.2. Let f : A → B be a function. Then the canonical equivalence relation θf of f is defined by
xθf y ⇐⇒ f(x) = f(y)
for all x,y ∈ A.
The set {θfx : x ∈ A} of equivalence classes of θf is called the quotient set of A with respect to f, written as A/θf , or simply quotient set, if f is understood.
Theorem 1.2. Let f : A → B be a function. Then, there are a set C, and functions g : A ։ C, h : C→ B such that g is surjective, h is injective, and f = h ◦ g.
The situation is picture in Figure 1.2
Figure 1.2: Mapping Theorem
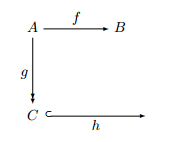
Proof. Set C = A/θf , and letg : A → A/θf be defined by x g→ θfx. Since each element of A is contained in exactly one class of E(θf ), h is a surjective function.
Now, let h : A/θf → B be defined as follows: Let t ∈ A/θf . Then, there is some x ∈ A, such that t = θfx; set h(t) = f(x). We need to show that the definition of h is independent of the choice of the representative x of the class t. Thus, let y ∈ θfx. By definition of θf , we have xθf y if and only if f(x) = f(y), and it follows that f(y) = f(x) for all y ∈ θfx.
Finally,
(g ◦ h)(x) = g(θfx) = f(x),
which proves our claim.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|