


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-1-2019
Date: 23-2-2019
Date: 23-2-2019
|
First of all, a rational function is pretty much just the division of two polynomial functions. For example, the following is a rational function:
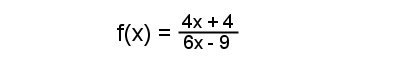
When adding or subtracting rational functions, you must find a common denominator as you might do with regular fractions. For example, to add 1/2 and 1/3, you might do the following:

Now, let's apply this same strategy to the addition and subtraction of rational functions:

Step 1) Find a common denominator by multiplying the denominators. So, (x + 3)(x - 2) becomes our common denominator in this case. Then, multiply each fraction by something equivalent to one, such as (x+3)/(x+3), to get each fraction in terms of that common denominator:
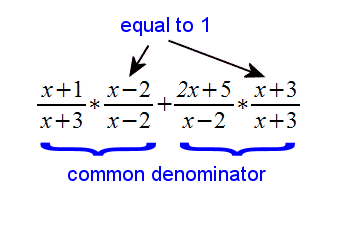
Here's what we have so far. Just multiply out the top and we will be ready to add the two fractions:
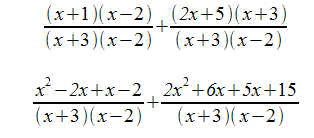
Now add the numerators just like you would with two simple fractions:
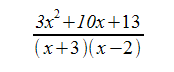
Finally we want to expand the denominator as well to give us the resulting rational function:
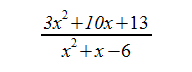
And that's our answer!
NOTE: To subtract rational functions, follow the same steps that you used to add rational functions, but just subtract the numerators instead of adding them!



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|