


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-1-2019
Date: 8-3-2017
Date: 17-2-2019
|
You probably know what a matrix is already if you are interested in matrix multiplication. However, a quick example won't hurt. A matrix is just a two-dimensional group of numbers. Instead of a list, called a vector, a matrix is a rectangle, like the following:
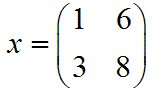
You can set a variable to be a matrix just as you can set a variable to be a number. In this case, x is the matrix containing those four numbers (in that particular order). Now, suppose you have two matrices that you need to multiply. Multiplication for numbers is pretty easy, but how do you do it for a matrix?
Here is a key point: You cannot just multiply each number by the corresponding number in the other matrix. Matrix multiplication is not like addition or subtraction. It is more complicated, but the overall process is not hard to learn. Here's an example first, and then I'll explain what I did:
Example:

Solution:
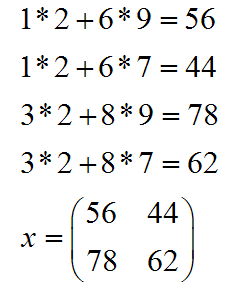
You're probably wondering how in the world I got that answer. Well you're justified in thinking that. Matrix multiplication is not an easy task to learn, and you do need to pay attention to avoid a careless error or two. Here's the process:

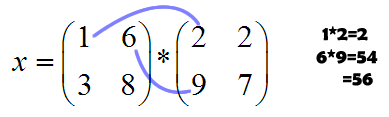
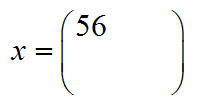

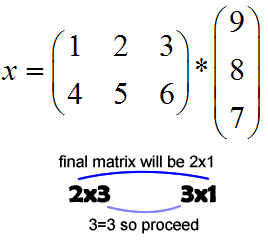
Now I know what you're thinking. That was really hard!!! Well it will seem that way until you get used to the process. It may help you to write out all your work, and even draw arrows to remember which way you're moving in the rows and columns. Just remember to multiply each row in the first matrix by each column in the second matrix.
What if the matrices aren't squares? Then you have to add another step. In order to multiply two matrices, the matrix on the left must have as many columns as the matrix on the right has rows. That way you can match up each pair while you're multiplying. The size of the final matrix is determined by the rows in the left matrix and the columns in the right. Here's what I do:
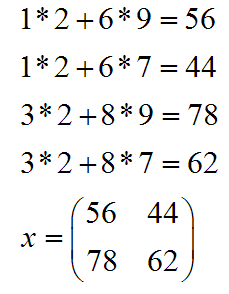
I write down the sizes of the matrices. The left matrix has 2 rows and 3 columns, so that's how we write it. Rows, columns, in that order. The other matrix is a 3x1 matrix because it has 3 rows and just 1 column. If the numbers in the middle match up you can multiply. The outside numbers give you the size of the answer. Even if you mess this up you'll figure it out eventually because you won't be able to multiply.
Here's an important reminder: Matrix Multiplication is not commutative. That means you cannot switch the order and expect the same result! Regular multiplication tells us that 4*3=3*4, but this is not multiplication of the usual sense.
Finally, here's an example with uneven matrix sizes to wrap things up:
Example:
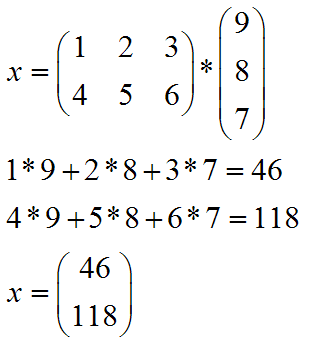



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
الطلبة المشاركون: مسابقة فنِّ الخطابة تمثل فرصة للتنافس الإبداعي وتنمية المهارات
|
|
|