


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 7-6-2017
التاريخ: 7-6-2017
التاريخ: 3-6-2017
التاريخ: 4-6-2017
|
الجريان الهدرومغناطيسي التحريكي
يشبه جريان البلازما في حقل مغنطيسي جريان سائل لزج او غاز من حيث انه يمكن ان يكون صفائحيا (laminar) او دواميا (turbulent). في اغلب الحالات يكون الحقل المغنطيسي موجها مع الجريان مانعا نشوء الحالة الدوامية او الاضطرابية او كما يقال يعمل على استقرار الحركة الصفائحية . ان الفعل الاستقراري لحقل مغنطيسي يظهر اقوى ما يمكن في حالة الناقلية العالية حيث يكون قانون التجمد قائما وعندئذ تؤدي الحركة الدوامية الى تشويه خطوط القوة المغنطيسية ونتيجة ذلك تتحول الطاقة الحركية الى طاقة مغنطيسية وفي البلازما الضعيفة الناقلية يعمل الحقل المغنطيسي ايضا على ممانعة تطور الحالة الدوامية لكن الية الاستقرار تختلف هنا عن سابقتها . فهذه الالية مرتبطة بكون انه عند حركة وسط ناقل في حقل مغنطيسي تثار(او تحرض) تيارات كهربائية التي تؤدي عند وجود ناقلية محدودة الى تبديد طاقة أي الى تحويل الطاقة الحركية الى حرارية الى (فعل جول) . وتحصل عملية مشابهة لبذل الطاقة في وسط غير الناقل على حساب اللزوجة . استنادا الى هذا التشابه يمكن تسمية المقدار c2/4π σ (معامل إنفاذية الحقل المغنطيسي) باللزوجة المغنطيسية.
تعرف طبيعة جريان السائل غير الناقل او الغاز بعدد رينولدس (Reynolds) اللابعدي أي:
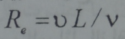
حيث Ʋ- سرعة التيار، L- بعد خطي، v- اللزوجة الحركية عند قيم صغيرة لعدد رينولدس تكون الحركة خطية. وعند قيم كبيرة تصبح دوامية. في التحريك الهدرومغنطيسي تتعلق طبقة الحركة ليس فقط بعدد بعدي واحد لا بعدي. اما اذا استبدلت اللزوجة الحركية في عدد رينولدس 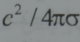 باللزوجة المغنطيسية فانه ينتج عدد رينولدس المغنطيسي اي:
باللزوجة المغنطيسية فانه ينتج عدد رينولدس المغنطيسي اي:
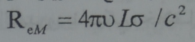
اذا كان عدد رينولدس المغنطيسي كبيرا فان الوسط الجاري يمكن اعتباره ذي ناقلية مثالية، واذا كان صغيرا فان الوسط يكزن سييء الناقلية.
في الحالة الحدية عندما يكون Rem ذا قيمة كبيرة فان طبيعة الحركة تتعين بنسبة الضغط المغنطيسي H2/8π الى علاقة السرعة 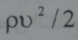 :
:
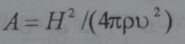
عند قيم كبيرة للعدد A (عمليا يكفي ان يكون اكبر من 0.1) يؤمن الحقل المغنطيسي استقرارية الجريان الخطي لبلازما جيدة الناقلية النظر عن عدد رينولدس.
في الحالة الحديدية عندما يكون Rem ذا قيمة صغيرة فان طبيعة الحركة تتعين بعدد ستيوارت S (Stewart) اللابعدي:
(S=AREM= H2σL/(C2Pv
اذا كانت قيمة هذا العدد تزيد على 0.1 فان الجريان الخطي يكون مستقرا عند اية قيمة لعدد رينولدس.
كل المقاييس الواردة تخص الجريان على طول الحقل المغنطيسي اما طبيعة الجريان وفق عرض الحقل المغنطيسي حسب القناة ذات العرض L فانها تتعين بقيمة عدد اخر لا بعدي ايضا هو عدد هارتمان (Hartman)

فعندما يأخذ عدد هارتمان قيما صغيرة فان الحركة تحصل كما في الحالة غياب حقل مغنطيسي . اما عند قيمة M كبيرة فان اللزوجة تبدي تأثيرا فقط طبقة رقيقة من مرتبة L/M المجاور بشكل مباشر لجدران القناة اما في بقية انحاء المقطع فان الحركة تحصل بسرعة ثابتة دون ان تتعلق بالبعد عن الجدران . عندها لن تتعلق مقاومة الحركة باللزوجة وتتعين بقوى كهرطيسية على نحو كامل.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|