
Comparing an Experimental Mean with a Known Value
 المؤلف:
D. A. Skoog, F. J.Holler, D M. West, and S. R. Crouch
المؤلف:
D. A. Skoog, F. J.Holler, D M. West, and S. R. Crouch
 المصدر:
Fundamentals of Analytical Chemistry
المصدر:
Fundamentals of Analytical Chemistry
 الجزء والصفحة:
9th. p 129
الجزء والصفحة:
9th. p 129
 4-5-2017
4-5-2017
 2421
2421
Comparing an Experimental Mean with a Known Value
There are many cases in which a scientist or engineer needs to compare the mean of a data set with a known value. In some cases, the known value is the true or accepted value based on prior knowledge or experience. An example is in comparing measured values of cholesterol to the value certified by NIST in a standard reference serum sample. In other situations, the known value might be a value predicted from theory or it might be a threshold value that we use in making decisions about the presence or absence of some constituent. An example of a decision-making value would be in comparing the measured mercury level in a bluefin tuna sample to the threshold toxicity level. In all these cases, we use a statistical hypothesis test to draw conclusions about the population mean m and its nearness to the known value, which we call μ0. There are two contradictory outcomes that we consider in any hypothesis test.
The first, the null hypothesis H0, states that μ = μ0. The second, the alternative hypothesis Ha can be stated in several ways. We might reject the null hypothesis in favor of Ha if m is different than μ0 (μ ≠ μ0). Other alternative hypotheses are μ < μ0 or μ > μ0. As a first example, suppose we are interested in determining whether the concentration of lead in an industrial wastewater discharge exceeds the maximum permissible amount of 0.05 ppm. Our hypothesis test would be summarized as:
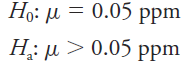
As a different example, suppose instead that experiments over a several-years period have determined that the mean lead level is 0.02 ppm. Recently, changes in the industrial process have been made, and we suspect that the mean lead level is now different than 0.02 ppm. In this instance, we do not care whether it is higher or lower than 0.02 ppm. Our hypothesis test would be summarized:

In order to apply the statistical test, a test procedure must be implemented. The crucial elements of a test procedure are the formation of an appropriate test statistic and the identification of a rejection region. The test statistic is formulated from the data on which we will base the decision to accept or reject H0. The rejection region consists of all the values of the test statistic for which H0 will be rejected. The null hypothesis is rejected if the test statistic lies within the rejection region. For tests concerning one or two means, the test statistic might be the z statistic if we have a large number of measurements or if we know σ. Quite often, however, we use the t statistic for small numbers of measurements with unknown σ. When in doubt, the t statistic should be used.
 الاكثر قراءة في مواضيع عامة في الكيمياء التحليلية
الاكثر قراءة في مواضيع عامة في الكيمياء التحليلية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


