
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The One-Electron Atom
المؤلف:
Donald A. Neamen
المصدر:
Semiconductor Physics and Devices
الجزء والصفحة:
p 45
9-5-2017
2346
The One-Electron Atom
The nucleus is a heavy, positively charged proton and the electron is a light. Negatively charged particle that, in the classical Bohr theory, is revolving around the nucleus. The potential function is due to the coulomb attraction between the proton and electron and is given by
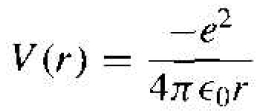 (1)
(1)
where e is the magnitude of the electronic charge and ϵ0 is the permittivity of free space. This potential function, although spherically symmetric, leads to a three dimensional problem in spherical coordinates.
We may generalize the time-independent Schrodinger's wave equation to three dimensions by writing
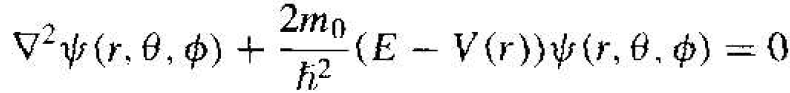 (2)
(2)
where 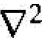 is the Laplacian operator and must be written in spherical coordinates for this case. The parameter m0 is the rest mass of the electron. In spherical coordinates, Schrodinger's wave equation may be written as
is the Laplacian operator and must be written in spherical coordinates for this case. The parameter m0 is the rest mass of the electron. In spherical coordinates, Schrodinger's wave equation may be written as
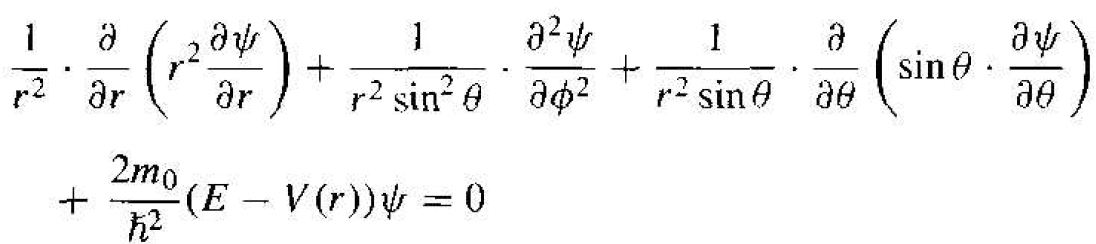 (3)
(3)
The solution to Equation (3) can be determined by the separation-of-variables technique. We will assume that the solution to the time-independent wave equation can be written in the form
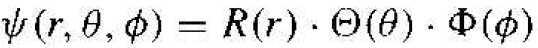 (4)
(4)
where R, Θ, and ɸ, are functions only of r, θ, and ϕ, respectively. Substituting this form of solution into Equation (3), we will obtain
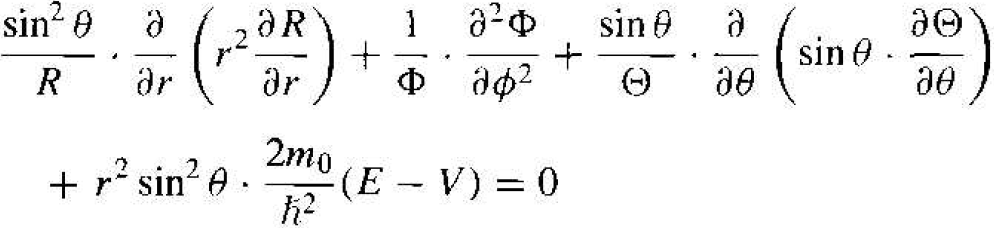 (5)
(5)
We may note that the second term in Equation (5) is a function of ϕ only, while all the other terms are functions of either r or θ. We may then write that
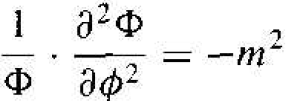 (6)
(6)
where m is a separation of variables constant. The solution to Equation (6) is of the form
 (7)
(7)
Since the wave function must be single-valued. we impose the condition that m is an integer, or
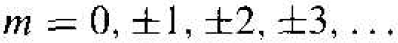 (8)
(8)
Incorporating the separation-of-variables constant we can further separate the variables θ and r and generate two additional separation-of-variables constants 1 and n. The separation-of-variables constants n, l, and m are known as quantum numbers and are related by
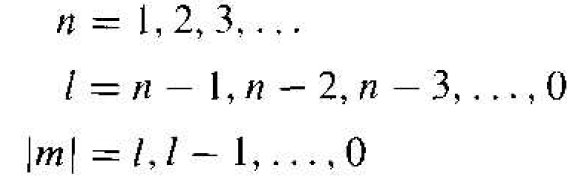 (9)
(9)
Each set of quantum numbers corresponds to a quantum state which the electron may occupy.
The electron energy may be written in the form
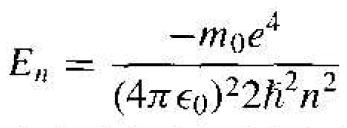 (10)
(10)
where n is the principal quantum number. The negative energy indicates that the electron is bound to the nucleus and we again see that the energy of the bound electron is quantized. If the energy were to become positive, then the electron would no longer be a bound panicle and the total energy would no longer be quantized. Since the parameter n in Equation (10) is an integer, the total energy of the electron can take on only discrete values. The quantized energy is again a result of the particle being bound in a finite region of space.
The solution of the wave equation may be designated by ѱn/m, where n, l, and m are again the various quantum numbers. For the lowest energy state, n = 1, l = 0, and m = 0, and the wave function is given by
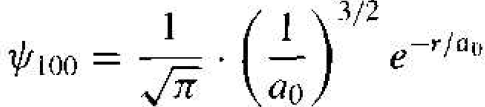 (11)
(11)
This function is spherically symmetric, and the parameter a0 is given by
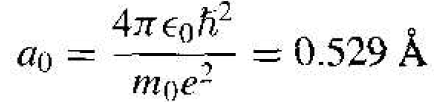 (12)
(12)
and is equal to the Bohr radius.
The radial probability density function, or the probability of finding the electron at a particular distance from the nucleus, is proportional to the product ѱ100 . ѱ*100 and also to the differential volume of the shell around the nucleus. The probability
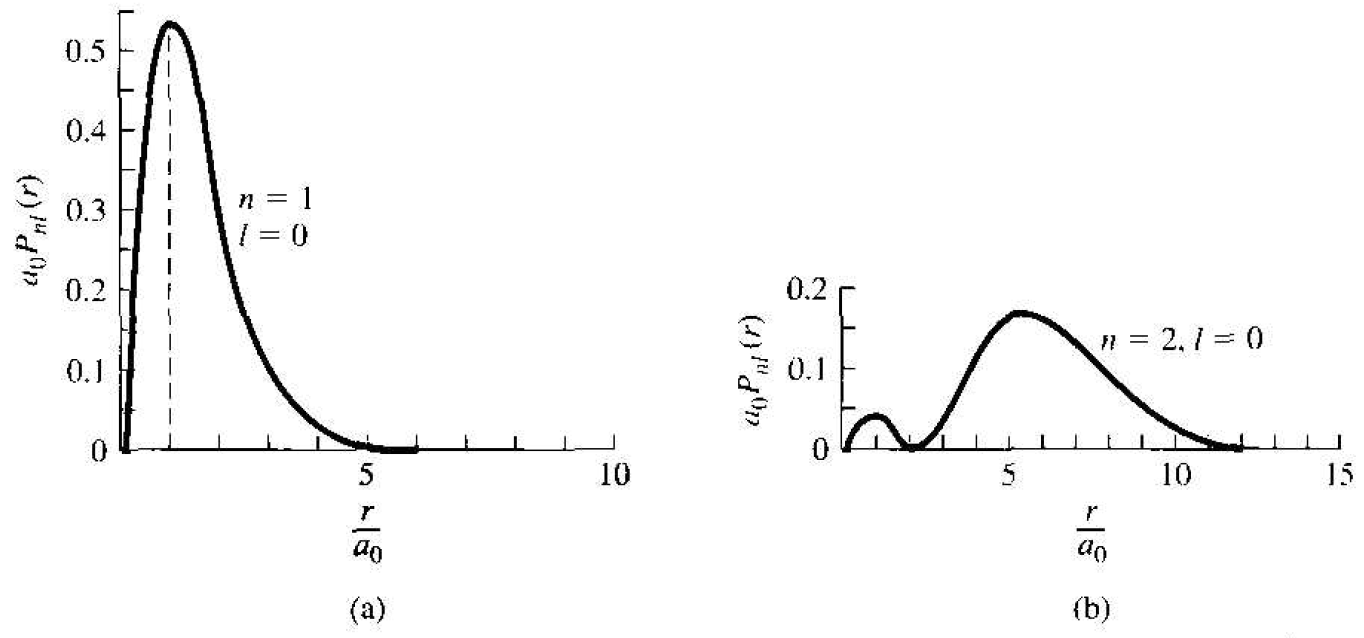
Figure 1.1 The radial probability density function for the one-electron atom in the (a) lowest energy state and (b) next-higher energy slate.
density function for the lowest energy state is plotted in Figure 1.1a. The most probable distance from the nucleus is at r = ao, which is the same as the Bohr theory. Considering this spherically symmetric probability function, we may now begin to conceive the concept of an electron cloud, or energy shell, surrounding the nucleus rather than a discrete particle orbiting around the nucleus.
The radial probability density function for the next higher, spherically symmetric wave function, corresponding to n = 2, l = 0. and m = 0, is shown in Figure 1.1b. This figure shows the idea of the next-higher energy shell of the electron. The second energy shell is at a greater radius from the nucleus than the first energy shell. As indicated in the figure, though, there is still a small probability that the electron will exist at the smaller radius. For the case of n = 2 and l = 1. there are three possible states corresponding to the three allowed values of the quantum number m. These wave functions are no longer spherically symmetric.
Although we have not gone into a great deal of mathematical detail for the one electron atom, three results are important for the further analysis of semiconductor materials. The first is the solution of Schrodinger's wave equation, which again yields electron probability functions, as it did for the simpler potential functions. In developing the physics of semiconductor materials in later chapters, we will also be considering electron probability functions. The second result is the quantization of allowed energy levels for the hound electron. The third is the concept of quantum numbers and quantum states, which evolved from the separation-of-variables technique. We will consider this concept again in the next section and in later chapters when we deal with the semiconductor material physics.
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















