


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-5-2021
Date: 19-6-2021
Date: 9-6-2021
|
Definition Let σ and τ be simplices in Rk . We say that τ is a face of σ if the set of vertices of τ is a subset of the set of vertices of σ. A face of σ is said to be a proper face if it is not equal to σ itself. An r-dimensional face of σ is referred to as an r-face of σ. A 1-dimensional face of σ is referred to as an edge of σ.
Note that any simplex is a face of itself. Also the vertices and edges of any simplex are by definition faces of the simplex.
Definition A finite collection K of simplices in Rk is said to be a simplicial complex if the following two conditions are satisfied:—
• if σ is a simplex belonging to K then every face of σ also belongs to K,
• if σ1 and σ2 are simplices belonging to K then either σ1 ∩ σ2 = ∅ or else σ1 ∩ σ2 is a common face of both σ1 and σ2.
The dimension of a simplicial complex K is the greatest non-negative integer n with the property that K contains an n-simplex. The union of all the simplices of K is a compact subset |K| of Rk referred to as the polyhedron of K. (The polyhedron is compact since it is both closed and bounded in Rk .)
Example Let Kσ consist of some n-simplex σ together with all of its faces.
Then Kσ is a simplicial complex of dimension n, and |Kσ| = σ.
Lemma 1.2 Let K be a simplicial complex, and let X be a topological space.
A function f: |K| → X is continuous on the polyhedron |K| of K if and only if the restriction of f to each simplex of K is continuous on that simplex.
Proof If a topological space can be expressed as a finite union of closed subsets, then a function is continuous on the whole space if and only if its restriction to each of the closed subsets is continuous on that closed set. The required result is a direct application of this general principle.
We shall denote by Vert K the set of vertices of a simplicial complex K (i.e., the set consisting of all vertices of all simplices belonging to K). A collection of vertices of K is said to span a simplex of K if these vertices are the vertices of some simplex belonging to K.
Definition: Let K be a simplicial complex in Rk . A subcomplex of K is a collection L of simplices belonging to K with the following property:
• if σ is a simplex belonging to L then every face of σ also belongs to L.
Note that every subcomplex of a simplicial complex K is itself a simplicial complex.
Definition Let v0, v1, . . . , vq be the vertices of a q-simplex σ in some Euclidean space Rk . We define the interior of the simplex σ to be the set of all points of σ that are of the form 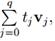 where tj > 0 for j = 0, 1, . . . , q and
where tj > 0 for j = 0, 1, . . . , q and 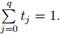 One can readily verify that the interior of the simplex σ consists of all points of σ that do not belong to any proper face of σ. (Note that, if σ ∈ Rk, then the interior of a simplex defined in this fashion will not coincide with the topological interior of σ unless dim σ = k.)
One can readily verify that the interior of the simplex σ consists of all points of σ that do not belong to any proper face of σ. (Note that, if σ ∈ Rk, then the interior of a simplex defined in this fashion will not coincide with the topological interior of σ unless dim σ = k.)
Note that any point of a simplex σ belongs to the interior of a unique face of σ. Indeed let v0, v1, . . . , vq be the vertices of σ, and let x ∈ σ. Then
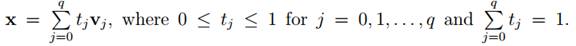
The unique face of σ containing x in its interior is then the face spanned by those vertices vj for which tj > 0.
Lemma 1.3 Let K be a finite collection of simplices in some Euclidean space Rk , and let |K| be the union of all the simplices in K. Then K is a simplicial complex (with polyhedron |K|) if and only if the following two conditions are satisfied:
• K contains the faces of its simplices,
• every point of |K| belongs to the interior of a unique simplex of K.
Proof Suppose that K is a simplicial complex. Then K contains the faces of its simplices. We must show that every point of |K| belongs to the interior of a unique simplex of K. Let x ∈ |K|. Then x belongs to the interior of a face σ of some simplex of K (since every point of a simplex belongs to the interior of some face). But then σ ∈ K, since K contains the faces of all its simplices. Thus x belongs to the interior of at least one simplex of K.
Suppose that x were to belong to the interior of two distinct simplices σ and τ of K. Then x would belong to some common face σ ∩ τ of σ and τ (since K is a simplicial complex). But this common face would be a proper face of one or other of the simplices σ and τ (since σ ≠τ ), contradicting the fact that x belongs to the interior of both σ and τ . We conclude that the simplex σ of K containing x in its interior is uniquely determined, as required.
Conversely, we must show that any collection of simplices satisfying the given conditions is a simplicial complex. Since K contains the faces of all its simplices, it only remains to verify that if σ and τ are any two simplices of K with non-empty intersection then σ ∩ τ is a common face of σ and τ .
Let x ∈ σ ∩ τ . Then x belongs to the interior of a unique simplex ω of K. However any point of σ or τ belongs to the interior of a unique face of that simplex, and all faces of σ and τ belong to K. It follows that ω is a common face of σ and τ , and thus the vertices of ω are vertices of both σ and τ . We deduce that the simplices σ and τ have vertices in common, and that every point of σ ∩ τ belongs to the common face ρ of σ and τ spanned by these common vertices. But this implies that σ ∩ τ = ρ, and thus σ ∩ τ is a common face of both σ and τ , as required.
Definition : A triangulation (K, h) of a topological space X consists of a simplicial complex K in some Euclidean space, together with a homeomorphism h: |K| → X mapping the polyhedron |K| of K onto X.
The polyhedron of a simplicial complex is a compact Hausdorff space. Thus if a topological space admits a triangulation then it must itself be a compact Hausdorff space.
Lemma 1.4 Let X be a Hausdorff topological space, let K be a simplicial complex, and let h: |K| → X be a bijection mapping |K| onto X. Suppose that the restriction of h to each simplex of K is continuous on that simplex. Then the map h: |K| → X is a homeomorphism, and thus (K, h) is a triangulation of X.
Proof Each simplex of K is a closed subset of |K|, and the number of simplices of K is finite. It follows from Lemma 1.2 that h: |K| → X is continuous.
Also the polyhedron |K| of K is a compact topological space. But every continuous bijection from a compact topological space to a Hausdorff space is a homeomorphism. Thus (K, h) is a triangulation of X.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|