


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 13-7-2017
Date: 13-7-2017
Date: 5-2-2021
|
Surface integrals
Let us take a surface S, which is not necessarily co-planar, and divide in up into (scalar) elements δSi. Then
 (1.1)
(1.1)
is a surface integral. For instance, the volume of water in a lake of depth D(x, y)
is
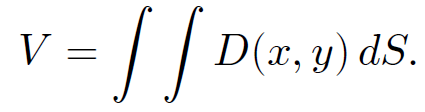 (1.2)
(1.2)
To evaluate this integral we must split the calculation into two ordinary integrals.
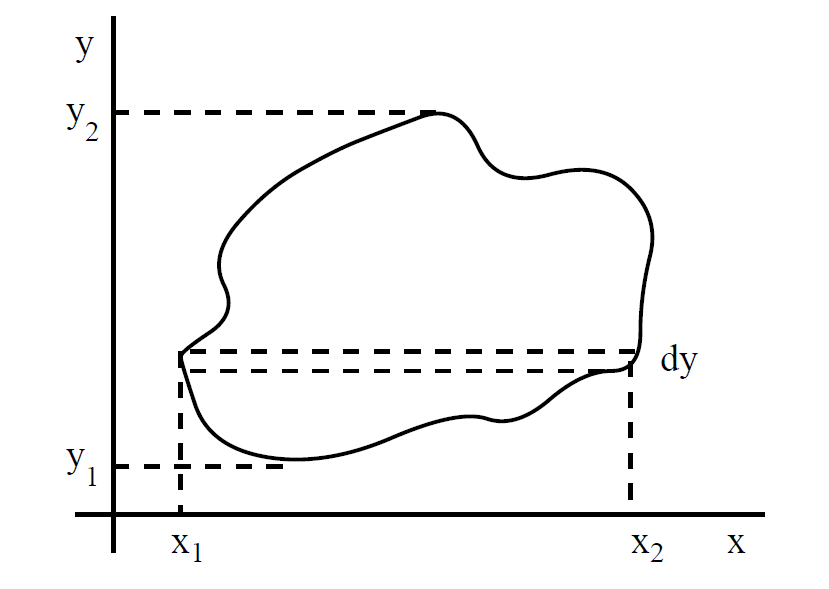
The volume in the strip shown in the diagram is
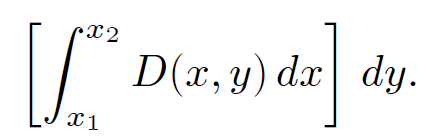 (1.3)
(1.3)
Note that the limits x1 and x2 depend on y. The total volume is the sum over all strips:
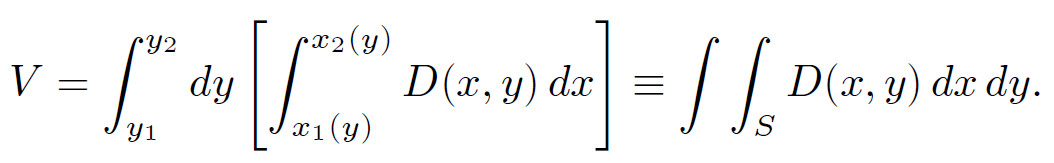 (1.4)
(1.4)
Of course, the integral can be evaluated by taking the strips the other way around:
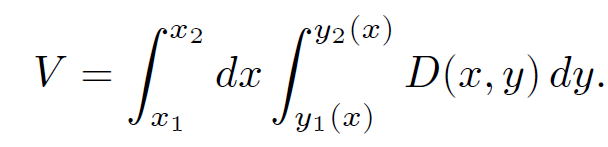 (1.5)
(1.5)
Interchanging the order of integration is a very powerful and useful trick. But great care must be taken when evaluating the limits. As an example, consider
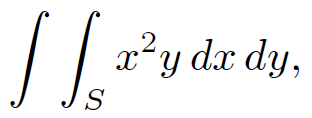 (1.6)
(1.6)
where S is shown in the diagram below. Suppose that we evaluate the x integral
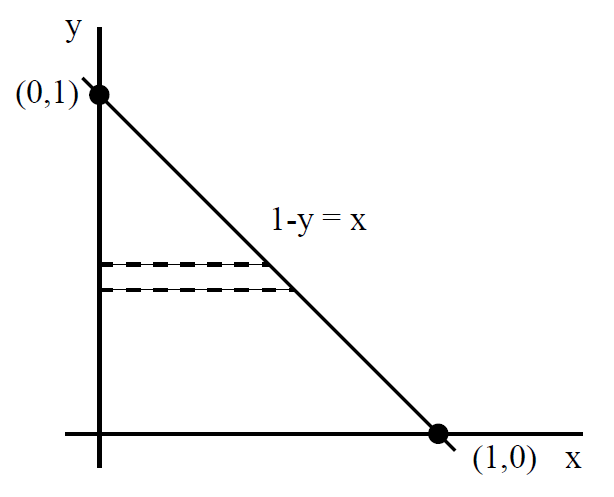
first:
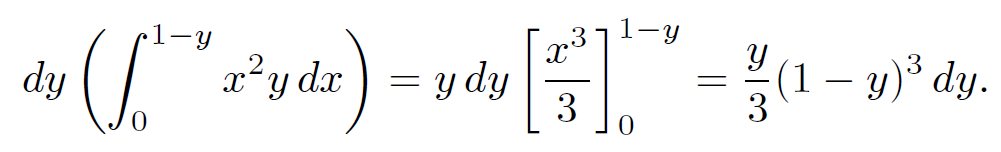 (1.7)
(1.7)
Let us now evaluate the y integral:
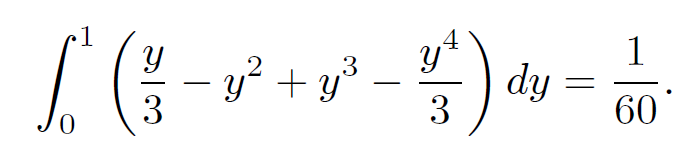 (1.8)
(1.8)
We can also evaluate the integral by interchanging the order of integration:
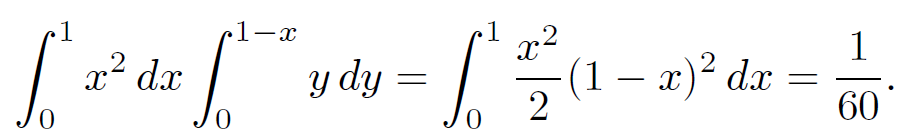 (1.9)
(1.9)
In some cases a surface integral is just the product of two separate integrals. For instance,
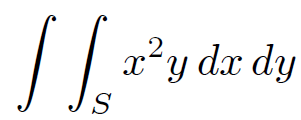 (1.10)
(1.10)
where S is a unit square. This integral can be written
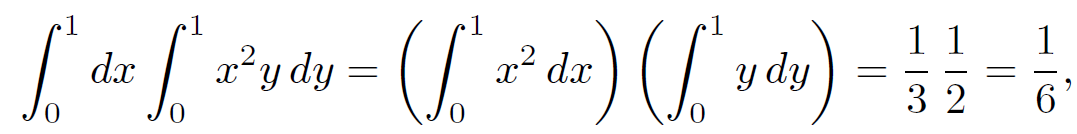 (1.11)
(1.11)
since the limits are both independent of the other variable. In general, when interchanging the order of integration the most important part of the whole problem is getting the limits of integration right. The only foolproof way of doing this is to draw a diagram.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|