

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Torsten Carleman
المؤلف:
G H Hardy
المصدر:
J E Littlewood and G Pólya
الجزء والصفحة:
...
27-7-2017
1449
Died: 11 January 1949 in Stockholm, Sweden

Tage Gills Torsten Carleman was born in the parish of Visseltofta, county of Kristianstad, in southern Sweden, where his father Karl Johan Carleman was a school teacher and precentor of the local church; his mother was Alma Linnéa Jungbeck. He finished his gymnasium studies in Växjö and was awarded his baccalaureate following the final high school graduation examination on 30 May 1910. In the same year he became a student at Uppsala University. He was awarded his Master of Science degree on 14 December 1912, Licentiate on 29 May 1915, and he defended his Ph.D. thesis On the Neumann-Poincaré problem for a region with corners on 20 January 1917 (undertaken with the supervision of Erik Holmgren), and became Doctor of Philosophy on 31 May 1917.
On 8 February 1917 he became a docent of mathematics at Uppsala University.
As a Liljewalch scholar he visited the Technical University in Zürich during the period 1 June 1917 to 31 March 1918, and also Paris and Oxford in 1921.
Carleman was a remarkable person and there are many stories concerning him (see Kjellberg [24], Garding [14]). We can quote here Kjellberg who has written in 1995 on page 93 of [24]:-
He was a genius! My older friends in Uppsala used to tell me about the wonderful years they had had when Carleman was there. He was the most active speaker in the Uppsala Mathematical Society. He was also a well-trained gymnast. When people left the seminar and on the way to the restaurant "Rullan" they had to cross the Fyris River, Carleman did not just walk over the bridge, instead he walked on his hands on the railing.
In 1923 he was appointed a full professor at Lund University. Shortly after this, on the initiative of Gösta Mittag-Leffler (who founded and gave his name to the famous mathematical research institute in Djursholm, Sweden), he was called as professor to Stockholm University in 1924, as a successor of Helge von Koch.
After Mittag-Leffler's death in 1927, Carleman, who was considered to be the top Swedish mathematician of the time, was appointed as the first director of the Mittag-Leffler Institute. He lived in the Mittag-Leffler villa and maintained the famous library. Many foreign scientists were guests at the Institute and gave lectures there, and the journal Acta Mathematica continued its publication of papers. However, Carleman was not able to realize plans for a Mathematics Institute, in part because of lack of funds and in part because his personality was more suited to mathematical contemplation than to the kind of entrepreneurship needed to get an Institute off the ground. For about twenty years after Carleman's death, the Institute was inactive and existed only as a growing library used by a handful of mathematicians in the Stockholm area and supervised by a member of the board, first F Carlson and then O Frostman (see [20] and [21], p. 1053).
We can quote here Garding [14], p. 206: -
From the beginning of the 1920s Carleman was considered the best mathematician in Sweden. International success came, but his spectral theory was overshadowed by the abstract theory and he had also bad luck with his mean ergodic theorem. It is certain that Carleman felt that he was the equal of the best mathematicians but also that he was not appreciated according to his merit. One reason was that many of his results, for instance the extension of Holmgren's uniqueness theorem, the analysis of the Schrödinger operator, and the existence theorem for Boltzmann's equation, were two decades ahead of their time and therefore not immediately appreciated.
From 1927 Carleman became an editor of Acta Mathematica. He was a member of the Royal Physiographic Society in Lund from 1924, the Royal Swedish Academy of Sciences from 1926, the Swedish Society of Sciences from 1927, the Finnish Society from 1934, and the French Society from 1946.
Carleman, giving a memorial address after death of Mittag-Leffler in 1927, told anecdotes about him and the famous benefactor Alfred Nobel (see [10], p. 81). When the latter was planning his prizes, he is said to have asked some mathematician:-
If I would establish a prize for Mathematics, is it likely that Mittag-Leffler would one day have it? - Yes, it is. - Well, then I won't do it.
Carleman had good relations with many mathematicians, visiting and giving lectures at, Zürich, Göttingen, Oxford, Sorbonne, Nancy and Paris. He was a frequent visitor to Paris.
Carleman had several Ph.D. students: N Juringius (1932), F Ehrnst (1938), K Persson (1938), A Pleijel (1940), U Hellsten (1947), and H Radström (1952).
He was married from 1929 to 1940 to Anna-Lisa Lemming (her father Erik Lemming was gold medalist in javelin throwing at the Olympic Games in Athens 1906, London 1908 and Stockholm 1912).
Carlson described Carleman in his obituary [16] (see also [14], p. 206) as:-
... retiring and taciturn, who looked at life and people with a bitter humour but he could also be kind and helpful to others, especially his students. Although not a natural athlete, he could perform amazing physical feats. Sometimes one got the impression of unbridled power both in his scientific and physical activity.
As it is often the case with mathematicians who deal with differential or integral equations, Carleman carried a keen interest in the relationship between mathematics and applied sciences. In 1944, at his demission of the presidency of the Royal Swedish Academy of Sciences, he gave a lecture On interaction between mathematics and exact experimental sciences (published in the Year Book of that Academy for the year 1944, pp. 263 - 273).
During the last period of his life Carleman lived alone in two rooms of the Mittag-Leffler Institute. His main interests had been mathematics and applied mathematics. Towards the end of the 1940's, when his health began to deteriorate he sometimes remarked to his students that (see [14], p. 206):-
... professors ought to be shot at the age of fifty.
Norbert Wiener in [7], pp. 317-318 has written:-
Carleman's death was peculiarly tragic, as it so typically followed a Scandinavian pattern which is familiar to those who know the plays of Ibsen and Strindberg. He died of drink - not the social drinking which leads so often to ruin here - but the fiery, passionate dipsomania which is a common disease even in the very best circles of the Scandinavian countries. During meetings he was often a bit drunk, and afterwards in Paris I saw him come to Mandelbrojt's apartment for an advance on the travel money due him, red-eyed, with a three-day beard.
During his last years Carleman suffered from bad health. Serious neuralgic pains in his legs often caused him insomnia. Towards Christmas 1948 a jaundice occurred, which quickly ended his life. Carleman died on 11 January 1949 in Stockholm.
Carleman published five books and sixty papers in mathematics. Before his professorship in Lund he published about thirty papers, the majority treating of the problems in the theory of integral equations, and the theory of real and complex functions, where he gave extraordinary evidence of originality, penetration and capacity to use various methods of analysis. Several of his new ideas and methods are now classical.
There are especially two areas of research, going back to this time, which one can consider as principal works of Carleman. One of them is his fundamental contribution on singular integral equations and applications. His first book Singular integral equations with real and symmetric kernel published in 1923 became fundamental. He was invited to give lectures on this subject at the Institute H Poincaré in Paris in the spring of 1930 and also at the International Congress of Mathematicians in Zürich in 1932.
The other was on quasi-analytic functions. Carleman was invited to lecture on this subject at the College of France in April-May 1923. His lectures were published later (in 1926) as his second book Quasi-analytic functions in Gauthier-Villars.
Carleman is now remembered for remarkable results in integral equations (1923), quasi-analytic functions (1926), harmonic analysis (1944), trigonometric series (1918-23), approximation of functions (1922-27) and Boltzmann's equation (1944). Names such as Carleman inequality, Carleman theorems (Denjoy-Carleman theorem on quasi-analytic classes of functions, Carleman theorem on conditions of well-definedness of moment problems, Carleman theorem on uniform approximation by entire functions, Carleman theorem on approximation of analytic functions by polynomials in the mean), Carleman singularity of orthogonal system, integral equation of Carleman type, Carleman operator, Carleman kernel, Carleman method of reducing an integral equation to a boundary value problem in the theory of analytic functions, Jensen-Carleman formula in complex analysis, Carleman continuum, Carleman linearization or Carleman embedding technique, Carleman polynomials, Carleman estimate in the unique continuation problem for solutions of partial differential equations and Carleman system in the kinetic theory of gas are well-known in mathematics (see [11], [14] and [9, Th. XII.17], [12], [13]).
The Carleman inequality was proved at the Scandinavian Congress of Mathematicians in Helsinki in 1922 (published in 1923) where Carleman was talking on quasi-analytic functions:
If (an), n ≥ 1, is a sequence of positive numbers, then
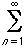 (a1. a2. ... .an)1/n≤ e an
(a1. a2. ... .an)1/n≤ e an
and the constant e is the best possible, in the sense that counterexamples can be constructed for any stricter inequality which uses a smaller constant.
There are many generalizations and applications of this inequality (cf. [6] and [22]).
In complex analysis there are Carleman formulae (proved already in 1926) which, unlike the Cauchy formula, reconstruct a function holomorphic in a domain D from its values on a part M of the boundary ∂D of a positive Lebesgue measure. Even in the case of one complex variable the Carleman formula depends on the domain D and on the set M.
Different generalizations as well as some applications of these formulae to various problems of mathematics (problems of analytic continuation in the theory of functions), in theoretical and mathematical physics, in extrapolation and interpolation of signals having a finite Fourier spectrum, and results obtained by computer simulation on the elimination of noise in a given frequency band, are presented in the book [13], which looks like an encyclopaedia on the theory and applications of the Carleman-type ideas and methods.
Carleman wrote also a Textbook in differential and integral calculus together with geometrical and mechanical applications, Stockholm 1928 (2nd ed. 1945).
In 1932 Carleman, following an idea of Poincaré, showed that a finite dimensional system of nonlinear differential equations d u/dt = V(u), where Vk are polynomials in u, can be embedded in an infinite system of linear differential equations. This is called Carleman linearization or Carleman embedding. This method has became a new effective tool in the study of nonlinear dynamical systems (see [12]).
Carleman is also one of the authors of a mean ergodic theorem (see [17], where more is written about priority questions).
Results on unique continuation for solutions to partial differential equations are important in many areas of applied mathematics, in particular in control theory and inverse problems. The unique continuation results as Holmgren and Hörmander theorems are based on a certain type of weighted energy estimate which was introduced by Carleman. In 1935 Carleman himself lectured at the Mittag-Leffler Institute on a generalization of the Fourier transformation. His notes, however, were not published until nine years later as his fourth book Fourier integral and questions connected with it in 1944 (reprinted in 1967). In June 1947 Carleman participated in a CNRS meeting in Nancy and presented his theory there. The connection of his and Schwartz's definition are nicely presented in [23].
Carleman lectured at the Sorbonne in 1937 on Boltzmann's equation, which appears in the kinetic theory of gas, and published several papers on this subject. Also his last book Mathematical problems of the kinetic theory of gas which deals with the mathematical aspects of the Boltzmann transport equation was published, after his death, in 1957 with some additional material submitted by L Carleson and O Frostman. This book was also translated into Russian in 1960.
- Biography in Svensk Uppslagsbok (Swedish Encyclopedia) (Swedish) (Malmö, 1947), 866. (first written by H Dalin and rewritten by N E Fremberg.)
- Biography in Bonniers Lexikon 3 (Swedish) (Stockholm, 1962), 73-74.
- Biography in A I Borodin and A S Bugai, Eminent mathematicians (Russian), (Kiev, 1987), 229.
- Biography in Nationalencyklopedin (Swedish) (Höganäs, 1990), 583.
- Biography in Lexicon of outstanding mathematicians (German) (Leipzig, 1990), 90. (written by A Vogt.)
Books:
- G H Hardy, J E Littlewood and G Pólya, Inequalities (Cambridge, 1934).
- N Wiener, I am a mathematician (Cambridge 1956).
Articles:
- Edition complete of articles of Torsten Carleman (French) (Malmö: Mittag-Leffler Mathematical Institute, Djursholm, 1960).
- M Reed and B Simon, Methods of modern mathematical physics IV : Analysis of operators (New York, 1978).
- G Elfving, The history of mathematics in Finland 1828-1918 (Helsinki, 1981).
- Encyclopaedia of Mathematics 2 (Kluwer 1988), 25-26.
- K Kowalski and W-H Steeb, Nonlinear dynamical systems and Carleman linearization (World Scientific, 1991).
- L A Aizenberg, Carleman's formulas in complex analysis : theory and applications (Kluwer, 1993).
- L Garding, Mathematics and mathematicians : mathematics in Sweden before 1950 (Providence, R.I., 1997).
- S Björk, Tage Gillis Torsten Carleman (Swedish), in Svenska Män och Kvinnor (Swedish Men and Women), Biographical Encyclopaedia 2 (Stockholm, 1946), 18.
- F Carlson, Obituary : Torsten Carleman (French), Acta Math. 82 (1950), i-vi. (Reprinted as Torsten Carleman in [8].)
- M Frank, Ergodic theory in the 1930's : a study in international mathematical activity (manuscript, Jan 2000).
- L Garding, Swedish Mathematicians (Swedish), Elementa 4 (1987), 182-190.
- H J Heyman, Tage Gillis Torsten Carleman (Swedish), in Svensk Biografiskt Lexikon (Swedish Biographical Dictionary) 7 (Bonniers förlag, 1927), 389-390.
- History of the Mittag-Leffler Institute, WEB page at:
- A Jackson, The Dream of a Swedish Mathematician : The Mittag-Leffler Institute, Notices Amer. Math. Soc. 46 (9) (1999), 1050-1058.
http://www.ams.org/notices/199909/fea-mittag.pdf - M Johansson, L E Persson and A Wedestig, Carleman's inequality - history, proofs and some new generalizations, J. Inequal. Pure Appl. Math. 4 (3) (2003), 1-19.
http://jipam.vu.edu.au/v4n3/135_02.html - C Kiselman, Generalized Fourier transformations : the work of Bochner and Carleman viewed in the light of the theories of Schwartz and Sato, in T Kawai and K Fujita (eds.), Microlocal Analysis and Complex Fourier Analysis (Singapore, 2002), 166-185.
- B Kjellberg, Mathematicians in Uppsala - some recollections (Swedish), in A Vretblad (ed.), Festschrift in honour of Lennart Carleson and Yngve Domar, Proc. Conf. at Dept. of Math., Uppsala Univ., May 1993 (Uppsala, 1995), 87-95.
 الاكثر قراءة في 1890to1894
الاكثر قراءة في 1890to1894
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















