
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
المعادلة العامة للمرايا الكروية
المؤلف:
محمد عطية سويلم، د. محمد روبين إدريس، بديع صالح الخطيب، د. أحمد يوسف قواسمة
المصدر:
الفيزياء العامة
الجزء والصفحة:
ص 292
28-12-2019
11284
المعادلة العامة للمرايا الكروية

الشكل (1)
يوضح الشكل (1) مرآة مقعرة موضوع أمامها جسم نقطي (A) ويصدر منه شعاعان : الشعاع (AQ) وينعكس هذا بحيث يلتقي مع المحور الرئيس في (A`) والشعاع (Av) يرتد على نفسه ، وبذلك يلتقى الشعاعان المنعكسان في (A`) ، وبذلك فإن خيال الجسم النقطي (A) هو (A`) دعنا الآن نتوصل إلى العلاقة التي تربط بين بعد الجسم عن المرآة (S) وبعد خياله عنها S`)) لتكن الزاوية التي يصنعها الشعاع مع المحور الرئيس (0) ولتكن الزاوية التي يصنعها (AQ) مع المحور الرئيس (u). والزاوية التي يصنعها (Qc) مع المحور الرئيس (u`) اذا كانت زاوية سقوط الشعاع (AQ) هي (Φ) ، فإن زاوية انعكاسه هي (`Φ) بحيث أن )Φ' = Φ( وبالاعتماد على الحقيقة أن الزاوية الخارجة للمثلث تساوي مجموع الزاويتين الداخلتين ما عدا المجاورة لها ، وبأخذ المثلثين (PQC) و (PQ`C) ، نحصل على :

وبحذف (Φ) من هاتين المعاملتين نحصل على :
وبحذف )Φ) من هاتين المعادلتين نحصل على :
(1) ……….. 
لننزل عمودا من (Q) على المحور الرئيس ، وليكن هذا العمود (Qv`) ، وليكن طول هذا العمود ((h والمسافة (vv`) هي s .
دعنا الآن نكتب العلاقات التي تعطي ظل كل من الزوايا , u` , uθ
(2)...........
وإذا كانت الزوايا , u` , u θ صغيرة ، فإنه يمكن تعويض قيم هذه الزوايا (بوجود الراديان) بدل ظلال هذه الزوايا ، كذلك اذا كانت (u) صغيرة ، فإن (s) صغيرة جدا لدرجة يمكن إهمالها وبذلك فان العلاقات لظلال الزوايا أعلاه تصبح كما يأتي :
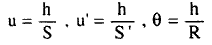 ...............(3)
...............(3)
وبتعويض قيم , u` , u θ من العلاقة (1) في العلاقات (3) وبالاختصار على (نحصل على) :
.(4).........
فإن العلاقة (4) تصبح كما يأتي :
.(5).........
تسمى العلاقة (4) أو العلاقة (5) المعاملة العامة للمرايا الكروية .
وعند استخدام أي من هاتين العلاقتين يؤخذ بعين الاعتبار ما يأتي :
1- (s) موجبة للجسم الحقيقي ، والجسم الحقيقي هي كل جسم (أو خيال جسم) تتفرق منه الأشعة الضوئية .
2- (s) سالبة للجسم الخيالي ، والجسم الخيالي هو أي جسم (أو خيال جسم) تتجمع
الأشعة الضوئية فيه .
3- (S`) موجبة للخيال الحقيقي وسالبة للخيال الوهمي .
4- (f) أو (R) موجبة للمرآة المقعرة وسالبة للمرآة المحدبة .
من الملاحظ أن حجم الخيال يختلف عن حجم الجسم في أغلب الأحيان ، فقد يكون الخيال اكبر وقد يكون أصغر ، لذا دعنا نتحدث عن التكبير ، في المرآة المقعرة أو المحدبة أو مجموعة من المرايا المقعرة والمحبة يساوي النسبة بين طول الخيال وطول الجسم سراء كان الخيال حقيقيا أم وهميا ، وسواء كان معتدلا أم مقلوبا . وبالرجوع إلى الشكل (١3-١0- أ) . فإن التكبير (M) يساوي :

أي أن التكبير في المرايا الكروية يساوي : 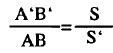
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















