The reciprocal of the arithmetic-geometric mean of 1 and ,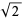

			(1)
			(2)
			(3)
			(4)
			(5)
			(6)
			(7)

(OEIS A014549), where 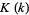 is the complete elliptic integral of the first kind,  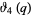is a Jacobi theta function, and  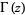is the gamma function. This correspondence was first noticed by Gauss, and was the basis for his exploration of the lemniscate function (Borwein and Bailey 2003, pp. 13-15).

Two rapidly converging series for 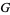 are given by

			(8)
			(9)

(Finch 2003, p. 421).

Gauss's constant has continued fraction [0, 1, 5, 21, 3, 4, 14, 1, 1, 1, 1, 1, 3, 1, 15, ...] (OEIS A053002).

The inverse of Gauss's constant is given by

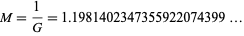(10)

(OEIS A053004; Finch 2003, p. 420; Borwein and Bailey 2003, p. 13), which has [1, 5, 21, 3, 4, 14, 1, 1, 1, 1, 1, 3, 1, 15, 1, ...] (OEIS A053003).

The value

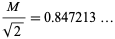(11)

(OEIS A097057) is sometimes called the ubiquitous constant (Spanier and Oldham 1987; Schroeder 1994; Finch 2003, p. 421), and

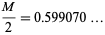(12)

(OEIS A076390) is sometimes called the second lemniscate constant (Finch 2003, p. 421).

Gauss's constants 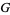 and 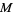 are related to the lemniscate constant  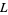by

			(13)
			(14)

(Finch 2003, p. 420).

REFERENCES:

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, p. 5, 1987.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.

Goldman, J. R. The Queen of Mathematics: An Historically Motivated Guide to Number Theory. Wellesley, MA: A K Peters, p. 92, 1997.

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.

Gosper, R. W. "A Calculus of Series Rearrangements." In Algorithms and Complexity: New Directions and Recent Results. Proc. 1976 Carnegie-Mellon Conference (Ed. J. F. Traub). New York: Academic Press, pp. 121-151, 1976.

Lewanowicz, S. and Paszowski, S. "An Analytic Method for Convergence Acceleration of Certain Hypergeometric Series." Math. Comput. 64, 691-713, 1995.

Schroeder, M. "How Probable is Fermat's Last Theorem?" Math. Intell. 16, 19-20, 1994.

Sloane, N. J. A. Sequences A014549, A053002, A053003, A053004, A076390, and A097057 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "The Kelvin Functions." Ch. 55 in An Atlas of Functions. Washington, DC: Hemisphere, 1987.

Todd, J. "The Lemniscate Constant." Comm. ACM 18, 14-19 and 462, 1975.