A twin Pythagorean triple is a Pythagorean triple 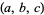 for which two values are consecutive integers. By definition, twin triplets are therefore primitive triples. Of the 16 primitive triples with hypotenuse less than 100, seven are twin triples. The first few twin triples, sorted by increasing 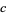, are (3, 4, 5), (5, 12, 13), (7, 24, 25), (20, 21, 29), (9, 40, 41), (11, 60, 61), (13, 84, 85), (15, 112, 113), ....

The numbers of twin triples with hypotenuse less than 10, 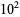, , 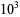... are 1, 7, 24, 74, ... (OEIS A101903).

The first few leg-leg triplets are (3, 4, 5), (20, 21, 29), (119, 120, 169), (696, 697, 985), ... (OEIS A001652, A046090, and A001653). A closed form is available for the 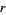th such pair. Consider the general reduced solution 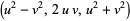, then the requirement that the legs be consecutive integers is

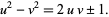(1)

Rearranging gives

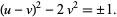(2)

Defining

			(3)
			(4)

then gives the Pell equation

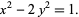(5)

Solutions to the Pell equation are given by

			(6)
			(7)

so the lengths of the legs 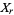 and 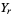 and the hypotenuse  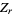are

			(8)
			(9)
			(10)
			(11)
			(12)
			(13)
			(14)
			(15)
			(16)

Denoting the length of the shortest leg by 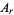 then gives

			(17)
			(18)

(Beiler 1966, pp. 124-125 and 256-257), which cannot be solved exactly to give 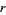 as a function of .

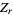However, the approximate number of leg-leg twin triplets 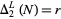 less than a given value of  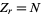can be found by noting that the second term in the denominator of  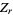is a small number to the power  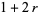and can therefore be dropped, leaving

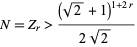(19)

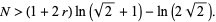(20)

Solving for 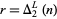 gives

			(21)
			(22)
			(23)

The first few leg-hypotenuse triples are (3, 4, 5), (5, 12, 13), (7, 24, 25), (9, 40, 41), (11, 60, 61), (13, 84, 85), ... (OEIS A005408, A046092, and A001844). Leg-hypotenuse twin triples 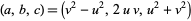 occur whenever

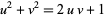(24)

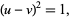(25)

that is to say when 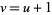, in which case the hypotenuse exceeds the even leg by unity and the twin triplet is given by 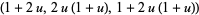. The number of leg-hypotenuse triplets with hypotenuse  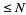is therefore given by

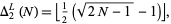(26)

where 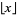 is the floor function. The first few values are 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, ... (OEIS A095861). The numbers of leg-hypotenuse triples less than 10, 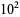, ... are 1, 6, 21, 70, 223, 706, 101904, ... (OEIS A101904).

The total number of twin triples 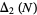 less than  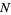is therefore approximately given by

			(27)
			(28)

where one has been subtracted to avoid double counting of the leg-leg-hypotenuse double-twin .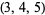

REFERENCES:

Beiler, A. H. "The Eternal Triangle." Ch. 14 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.

Sloane, N. J. A. Sequences A001652/M3074, A001653/M3955, A001844/M3826, A005408/M2400, A046090, A046092, A095861, A101903, A101904 in "The On-Line Encyclopedia of Integer Sequences."