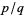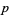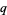An irrational number is a number that cannot be expressed as a fraction  for any integers  and . Irrational numbers have decimal expansions that neither terminate nor become periodic. Every transcendental number is irrational.

There is no standard notation for the set of irrational numbers, but the notations , , 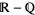or 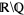, where the bar, minus sign, or backslash indicates the set complement of the rational numbers  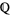over the reals 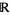, could all be used.

The most famous irrational number is 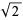, sometimes called Pythagoras's constant. Legend has it that the Pythagorean philosopher Hippasus used geometric methods to demonstrate the irrationality of  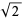while at sea and, upon notifying his comrades of his great discovery, was immediately thrown overboard by the fanatic Pythagoreans. Other examples include 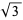, , 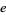, 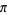etc. The Erdős-Borwein constant

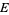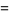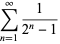			(1)
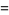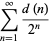			(2)
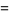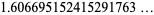			(3)

(OEIS A065442; Erdős 1948, Guy 1994), where 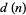 is the numbers of divisors of 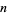, and a set of generalizations (Borwein 1992) are also known to be irrational (Bailey and Crandall 2002).

Numbers of the form 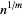 are irrational unless  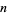is the 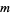th power of an integer. Numbers of the form 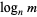, where  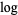is the logarithm, are irrational if  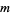and 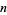 are integers, one of which has a prime factor which the other lacks.  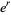is irrational for rational 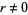.  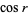is irrational for every rational number  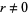(Niven 1956, Stevens 1999), and  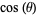(for 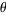 measured in degrees) is irrational for every rational  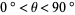with the exception of  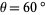(Niven 1956).  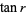is irrational for every rational  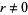(Stevens 1999).

The irrationality of e was proven by Euler in 1737; for the general case, see Hardy and Wright (1979, p. 46). 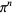 is irrational for positive integral 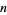. The irrationality of pi itself was proven by Lambert in 1760; for the general case, see Hardy and Wright (1979, p. 47). Apéry's constant  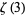(where  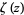is the Riemann zeta function) was proved irrational by Apéry (1979; van der Poorten 1979). In addition, T. Rivoal (2000) recently proved that there are infinitely many integers  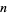such that  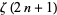is irrational. Subsequently, he also showed that at least one of 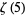, , 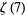...,  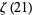is irrational (Rivoal 2001).

From Gelfond's theorem, a number of the form 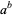 is transcendental (and therefore irrational) if  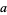is algebraic 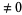, 1 and  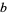is irrational and algebraic. This establishes the irrationality of Gelfond's constant  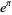(since 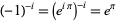), and 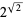. Nesterenko (1996) proved that  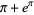is irrational. In fact, he proved that 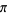,  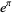and 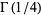 are algebraically independent, but it was not previously known that  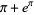was irrational.

Given a polynomial equation

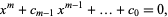(4)

where 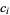 are integers, the roots  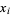are either integral or irrational. If  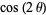is irrational, then so are 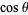, , 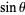and .

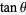Irrationality has not yet been established for 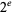, , 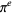, 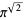or 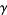 (where  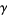is the Euler-Mascheroni constant).

Quadratic surds are irrational numbers which have periodic continued fractions.

Hurwitz's irrational number theorem gives bounds of the form

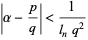(5)

for the best rational approximation possible for an arbitrary irrational number 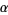, where the  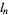are called Lagrange numbers and get steadily larger for each "bad" set of irrational numbers which is excluded.

The series

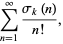(6)

where 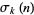 is the divisor function, is irrational for  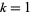and 2.

REFERENCES:

Apéry, R. "Irrationalité de 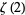 et 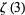." Astérisque 61, 11-13, 1979.

Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.

Preprint dated Feb. 22, 2003 available at https://www.nersc.gov/~dhbailey/dhbpapers/bcnormal.pdf.

Borwein, P. "On the Irrationality of Certain Series." Math. Proc. Cambridge Philos. Soc. 112, 141-146, 1992.

Courant, R. and Robbins, H. "Incommensurable Segments, Irrational Numbers, and the Concept of Limit." §2.2 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 58-61, 1996.

Erdős, P. "On Arithmetical Properties of Lambert Series." J. Indian Math. Soc. 12, 63-66, 1948.

Gourdon, X. and Sebah, P. "Irrationality Proofs." https://numbers.computation.free.fr/Constants/Miscellaneous/irrationality.html.

Guy, R. K. "Some Irrational Series." §B14 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 69, 1994.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Huylebrouck, D. "Similarities in Irrationality Proofs for 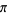, , 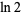, 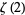and 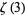." Amer. Math. Monthly 108, 222-231, 2001.

Manning, H. P. Irrational Numbers and Their Representation by Sequences and Series. New York: Wiley, 1906.

Nagell, T. "Irrational Numbers" and "Irrationality of the numbers 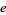 and 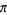." §12-13 in Introduction to Number Theory. New York: Wiley, pp. 38-40, 1951.

Nesterenko, Yu. "Modular Functions and Transcendence Problems." C. R. Acad. Sci. Paris Sér. I Math. 322, 909-914, 1996.

Nesterenko, Yu. V. "Modular Functions and Transcendence Questions." Mat. Sb. 187, 65-96, 1996.

Niven, I. M. Irrational Numbers. New York: Wiley, 1956.

Niven, I. M. Numbers: Rational and Irrational. New York: Random House, 1961.

Pappas, T. "Irrational Numbers & the Pythagoras Theorem." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 98-99, 1989.

Rivoal, T. "La fonction Zeta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs." Comptes Rendus Acad. Sci. Paris 331, 267-270, 2000.

Rivoal, T. "Irrationalité d'au moins un des neuf nombres 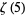, , 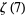..., 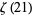." 25 Apr 2001. https://arxiv.org/abs/math.NT/0104221.

Sloane, N. J. A. Sequence A065442 in "The On-Line Encyclopedia of Integer Sequences."

Stevens, J. "Zur Irrationalität von 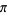." Mitt. Math. Ges. Hamburg 18, 151-158, 1999.

van der Poorten, A. "A Proof that Euler Missed... Apéry's Proof of the Irrationality of 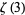." Math. Intel. 1, 196-203, 1979.

Weisstein, E. W. "Books about Irrational Numbers." https://www.ericweisstein.com/encyclopedias/books/IrrationalNumbers.html.