Legendre-Gauss Quadrature
المؤلف:
Abbott, P
المصدر:
"Tricks of the Trade: Legendre-Gauss Quadrature." Mathematica J. 9
الجزء والصفحة:
...
5-12-2021
1012
Legendre-Gauss Quadrature
Legendre-Gauss quadrature is a numerical integration method also called "the" Gaussian quadrature or Legendre quadrature. A Gaussian quadrature over the interval ![[-1,1]](https://mathworld.wolfram.com/images/equations/Legendre-GaussQuadrature/Inline1.gif)
with weighting function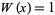 
. The abscissas for quadrature order 
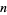are given by the roots of the Legendre polynomials 
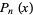, which occur symmetrically about 0. The weights are
where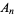 
is the coefficient of 
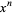in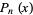 
. For Legendre polynomials,
 |
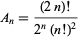(3)
|
(Hildebrand 1956, p. 323), so
Additionally,
(Hildebrand 1956, p. 324), so
Using the recurrence relation
(correcting Hildebrand 1956, p. 324) gives
(Hildebrand 1956, p. 324).
The weights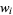 
satisfy
 |
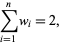(14)
|
which follows from the identity
![sum_(nu=1)^n(1-x_nu^2)/((n+1)^2[P_(n+1)(x_nu)]^2)=1.](https://mathworld.wolfram.com/images/equations/Legendre-GaussQuadrature/NumberedEquation3.gif) |
(15)
|
The error term is
![E=(2^(2n+1)(n!)^4)/((2n+1)[(2n)!]^3)f^((2n))(xi).](https://mathworld.wolfram.com/images/equations/Legendre-GaussQuadrature/NumberedEquation4.gif) |
(16)
|
Beyer (1987) gives a table of abscissas and weights up to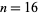 
, and Chandrasekhar (1960) up to 
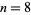for 
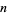even.
 |
 |
 |
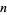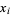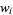| 2 |
 |
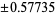1.000000 |
| 3 |
0 |
0.888889 |
| |
 |
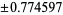0.555556 |
| 4 |
 |
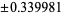0.652145 |
| |
 |
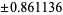0.347855 |
| 5 |
0 |
0.568889 |
| |
 |
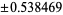0.478629 |
| |
 |
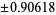0.236927 |
The exact abscissas are given in the table below.
The abscissas for order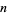 
quadrature are roots of the Legendre polynomial 
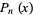, meaning they are algebraic numbers of degrees 1, 2, 2, 4, 4, 6, 6, 8, 8, 10, 10, 12, ..., which is equal to 
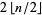for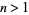 
(OEIS A052928).
Similarly, the weights for order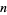 
quadrature can be expressed as the roots of polynomials of degree 1, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, ..., which is equal to 
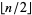for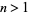 
(OEIS A008619). The triangle of polynomials whose roots determine the weights is
 |
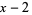(17)
|
 |
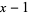(18)
|
 |
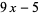(19)
|
 |
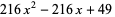(20)
|
 |
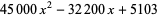(21)
|
 |
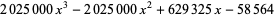(22)
|
 |
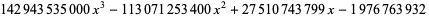(23)
|
 |
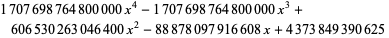(24)
|
REFERENCES:
Abbott, P. "Tricks of the Trade: Legendre-Gauss Quadrature." Mathematica J. 9, 689-691, 2005.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 462-463, 1987.
Chandrasekhar, S. Radiative Transfer. New York: Dover, pp. 56-62, 1960.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 323-325, 1956.
Sloane, N. J. A. Sequences A008619, A052928, and A112734 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في التحليل العددي
اخر الاخبار
اخبار العتبة العباسية المقدسة
