
Sturm Function
 المؤلف:
Acton, F. S
المؤلف:
Acton, F. S
 المصدر:
Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer
المصدر:
Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer
 الجزء والصفحة:
...
الجزء والصفحة:
...
 14-12-2021
14-12-2021
 1826
1826
Sturm Function
Given a function 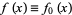 , write
, write 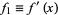 and define the Sturm functions by
and define the Sturm functions by
![f_n(x)=-<span style=]() {f_(n-2)(x)-f_(n-1)(x)[(f_(n-2)(x))/(f_(n-1)(x))]}, " src="https://mathworld.wolfram.com/images/equations/SturmFunction/NumberedEquation1.gif" style="height:38px; width:233px" /> {f_(n-2)(x)-f_(n-1)(x)[(f_(n-2)(x))/(f_(n-1)(x))]}, " src="https://mathworld.wolfram.com/images/equations/SturmFunction/NumberedEquation1.gif" style="height:38px; width:233px" /> |
(1)
|
where ![[P(x)/Q(x)]](https://mathworld.wolfram.com/images/equations/SturmFunction/Inline3.gif) is a polynomial quotient. Then construct the following chain of Sturm functions,
is a polynomial quotient. Then construct the following chain of Sturm functions,
known as a Sturm chain. The chain is terminated when a constant 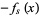 is obtained.
is obtained.
Sturm functions provide a convenient way for finding the number of real roots of an algebraic equation with real coefficients over a given interval. Specifically, the difference in the number of sign changes between the Sturm functions evaluated at two points 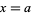 and
and 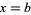 gives the number of real roots in the interval
gives the number of real roots in the interval 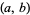 . This powerful result is known as the Sturm theorem. However, when the method is applied numerically, care must be taken when computing the polynomial quotients to avoid spurious results due to roundoff error.
. This powerful result is known as the Sturm theorem. However, when the method is applied numerically, care must be taken when computing the polynomial quotients to avoid spurious results due to roundoff error.
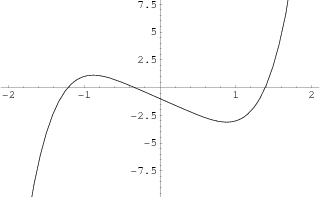
As a specific application of Sturm functions toward finding polynomial roots, consider the function 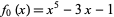 , plotted above, which has roots
, plotted above, which has roots 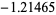 ,
, 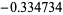 ,
, 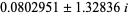 , and 1.38879 (three of which are real). The derivative is given by
, and 1.38879 (three of which are real). The derivative is given by 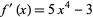 , and the Sturm chain is then given by
, and the Sturm chain is then given by
The following table shows the signs of 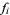 and the number of sign changes
and the number of sign changes 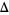 obtained for points separated by
obtained for points separated by 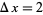 .
.
 |
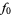 |
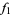 |
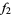 |
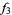 |
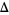 |
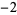 |
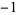 |
1 |
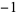 |
1 |
3 |
| 0 |
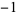 |
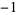 |
1 |
1 |
1 |
| 2 |
1 |
1 |
1 |
1 |
0 |
This shows that 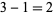 real roots lie in
real roots lie in 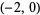 , and
, and 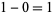 real root lies in
real root lies in 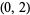 . Reducing the spacing to
. Reducing the spacing to 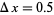 gives the following table.
gives the following table.
 |
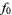 |
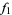 |
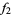 |
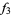 |
 |
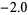 |
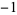 |
1 |
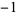 |
1 |
3 |
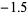 |
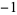 |
1 |
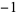 |
1 |
3 |
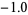 |
1 |
1 |
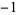 |
1 |
2 |
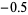 |
1 |
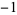 |
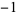 |
1 |
2 |
| 0.0 |
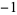 |
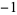 |
1 |
1 |
1 |
| 0.5 |
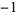 |
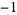 |
1 |
1 |
1 |
| 1.0 |
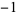 |
1 |
1 |
1 |
1 |
| 1.5 |
1 |
1 |
1 |
1 |
0 |
| 2.0 |
1 |
1 |
1 |
1 |
0 |
This table isolates the three real roots and shows that they lie in the intervals 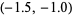 ,
, 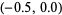 , and
, and 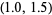 . If desired, the intervals in which the roots fall could be further reduced.
. If desired, the intervals in which the roots fall could be further reduced.
The Sturm functions satisfy the following conditions:
1. Two neighboring functions do not vanish simultaneously at any point in the interval.
2. At a null point of a Sturm function, its two neighboring functions are of different signs.
3. Within a sufficiently small interval surrounding a zero point of 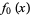 ,
, 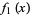 is everywhere greater than zero or everywhere smaller than zero.
is everywhere greater than zero or everywhere smaller than zero.
REFERENCES:
Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., p. 334, 1990.
Dörrie, H. "Sturm's Problem of the Number of Roots." §24 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 112-116, 1965.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, p. 469, 1992.
Rusin, D. "Known Math." http://www.math.niu.edu/~rusin/known-math/96/sturm.
Sturm, C. "Mémoire sur la résolution des équations numériques." Bull. des sciences de Férussac 11, 1929.
 الاكثر قراءة في التحليل العددي
الاكثر قراءة في التحليل العددي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


