Hermite-Gauss Quadrature
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
12-12-2021
1582
Hermite-Gauss Quadrature
Hermite-Gauss quadrature, also called Hermite quadrature, is a Gaussian quadrature over the interval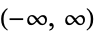 
with weighting function 
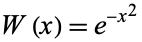(Abramowitz and Stegun 1972, p. 890). The abscissas for quadrature order 
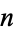are given by the roots 
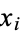of the Hermite polynomials 
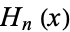, which occur symmetrically about 0. The weights are
where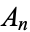 
is the coefficient of 
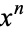in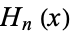 
. For Hermite polynomials,
 |
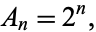(3)
|
so
 |
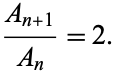(4)
|
Additionally,
 |
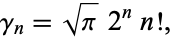(5)
|
so
where (8) and (9) follow using the recurrence relation
 |
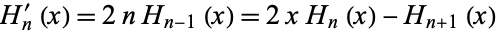(11)
|
to obtain
 |
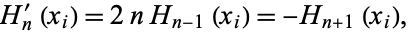(12)
|
and (10) is from Abramowitz and Stegun (1972 p. 890).
The error term is
 |
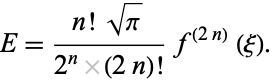(13)
|
Beyer (1987) gives a table of abscissas and weights up to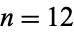 
.
 |
 |
 |
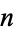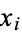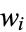| 2 |
 |
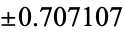0.886227 |
| 3 |
0 |
1.18164 |
| |
 |
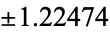0.295409 |
| 4 |
 |
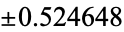0.804914 |
| |
 |
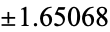0.0813128 |
| 5 |
0 |
0.945309 |
| |
 |
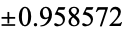0.393619 |
| |
 |
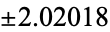0.0199532 |
The abscissas and weights can be computed analytically for small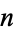 
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 890, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 464, 1987.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 327-330, 1956.
الاكثر قراءة في التحليل العددي
اخر الاخبار
اخبار العتبة العباسية المقدسة
