
Euler-Maclaurin Integration Formulas
 المؤلف:
Abramowitz, M. and Stegun, I. A.
المؤلف:
Abramowitz, M. and Stegun, I. A.
 المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
 الجزء والصفحة:
...
الجزء والصفحة:
...
 9-12-2021
9-12-2021
 2490
2490
Euler-Maclaurin Integration Formulas
The Euler-Maclaurin integration and sums formulas can be derived from Darboux's formula by substituting the Bernoulli polynomial 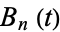 in for the function
in for the function 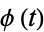 . Differentiating the identity
. Differentiating the identity
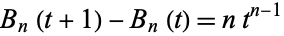 |
(1)
|
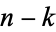 times gives
times gives
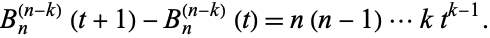 |
(2)
|
Plugging in 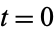 gives
gives 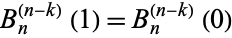 . From the Maclaurin series of
. From the Maclaurin series of 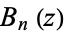 with
with 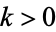 , we have
, we have
where 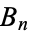 is a Bernoulli number, and substituting these values of
is a Bernoulli number, and substituting these values of 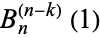 and
and 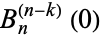 into Darboux's formula gives
into Darboux's formula gives
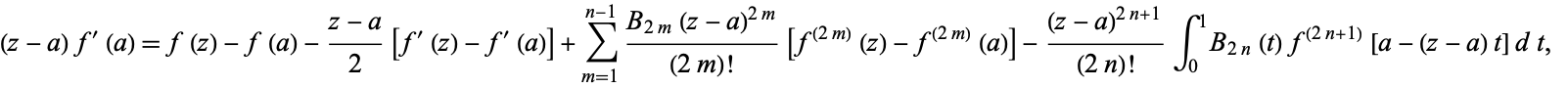 |
(7)
|
which is the Euler-Maclaurin integration formula (Whittaker and Watson 1990, p. 128). It holds when the function 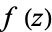 is analytic in the integration region
is analytic in the integration region
In certain cases, the last term tends to 0 as 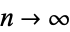 , and an infinite series can then be obtained for
, and an infinite series can then be obtained for 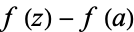 . In such cases, sums may be converted to integrals by inverting the formula to obtain the Euler-Maclaurin sum formula
. In such cases, sums may be converted to integrals by inverting the formula to obtain the Euler-Maclaurin sum formula
![sum_(k=1)^(n-1)f_k=int_0^nf(k)dk-1/2[f(0)+f(n)]+sum_(k=1)^infty(B_(2k))/((2k)!)[f^((2k-1))(n)-f^((2k-1))(0)],](https://mathworld.wolfram.com/images/equations/Euler-MaclaurinIntegrationFormulas/NumberedEquation4.gif) |
(8)
|
which, when expanded, gives
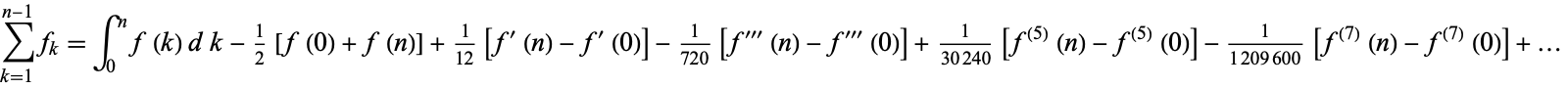 |
(9)
|
(Abramowitz and Stegun 1972, p. 16). The Euler-Maclaurin sum formula is implemented in the Wolfram Language as the function NSum with option Method -> "EulerMaclaurin".
The second Euler-Maclaurin integration formula is used when 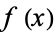 is tabulated at
is tabulated at 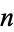 values
values 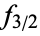 ,
, 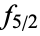 , ...,
, ..., 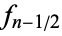 :
:
![int_(x_1)^(x_n)f(x)dx=h[f_(3/2)+f_(5/2)+f_(7/2)+...+f_(n-3/2)+f_(n-1/2)]
-sum_(k=1)^infty(B_(2k)h^(2k))/((2k)!)(1-2^(-2k+1))[f_n^((2k-1))-f_1^((2k-1))].](https://mathworld.wolfram.com/images/equations/Euler-MaclaurinIntegrationFormulas/NumberedEquation6.gif) |
(10)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 16 and 806, 1972.
Apostol, T. M. "An Elementary View of Euler's Summation Formula." Amer. Math. Monthly 106, 409-418, 1999.
Arfken, G. "Bernoulli Numbers, Euler-Maclaurin Formula." §5.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 327-338, 1985.
Borwein, J. M.; Borwein, P. B.; and Dilcher, K. "Pi, Euler Numbers, and Asymptotic Expansions." Amer. Math. Monthly 96, 681-687, 1989.
Euler, L. Comm. Acad. Sci. Imp. Petrop. 6, 68, 1738.
Havil, J. "Euler-Maclaurin Summation." §10.2 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 85-86, 2003.
Knopp, K. Theory and Application of Infinite Series. New York: Dover, 1990.
Maclaurin, C. Treatise of Fluxions. Edinburgh, p. 672, 1742.
Vardi, I. "The Euler-Maclaurin Formula." §8.3 in Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 159-163, 1991.
Whittaker, E. T. and Robinson, G. "The Euler-Maclaurin Formula." §67 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 134-136, 1967.
Whittaker, E. T. and Watson, G. N. "The Euler-Maclaurin Expansion." §7.21 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 127-128, 1990.
 الاكثر قراءة في التحليل العددي
الاكثر قراءة في التحليل العددي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


