مخططات الطاقة في مناطق الحقول المتوسطة: العزوم المغناطيسية الفعالة
المؤلف:
الدكتور محمد انور بطل
المصدر:
الفيزياء الذرية والجزيئية
الجزء والصفحة:
ص 201
10-2-2022
1804
مخططات الطاقة في مناطق الحقول المتوسطة: العزوم المغناطيسية الفعالة
لقد كانت الدراسة محدودة في حالة الحقل الضعيف ، الحقل القوي لكن في حالات ذرات ذات سبين نووي فإن البنيات الفوق ناعمة تكون ضعيفة, جداً ، مرتبة بعض الميغاسيكل / ثانية ، وبين العشرات الألوف الميغاسيكل / ثانية ، مع عامل لانده g=1 فإن فرق الطاقة بين مستويين جزيئين لزيمان متعاقبان هو 1.4MHzعلى غوص ، ومن المحتمل جداً أنه ضمن شروط الحقل المغناطيسي فإن التقاريب يمكن أن نتحقق ، والعديد من التجارب في علم الطيوف ذات الترددات الراديوية تمت ضمن شروط الحقل المتوسط (ما بين) ، إذاً يجب تطبيق الإضطراب w + T3 على حلول Ho+T1+T2.
كما رأينا إن الحلول يجب أن يعبر عنها كتابع ل mF= mI + mJ باعتبار أن الكمية المحفوظة مهما كان الحقل هي العزم الحركي الكلي F.
الحل تحليلياً غير ممكن وعددياً فقط يتم الحصول عليه ، إلا أنه في الحالة الخاصة حيث J أو I مساوياً 1/2 يمكن إيجاد حل تحليلي . لنحدد هذه العلاقة من أجل مستوي I, J = 1/2 تأخذ أي قيمة:
لندعو (F, mF) E الطاقة ضمن الحقل B لذرة ذات عزم حركي كلي F ، ومميزة بالعدد
mF= mI + mJ
Eo الطاقة المحسوبة بدون الأخذ بعين الإعتبار للبنية الناعمة. أخيراً لندخل بدل الحقل المغناطيسي B البارامتر (المتحول) χ:
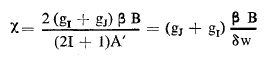
(وذلك بتسمية 'Sw= (2I + 1)/(2)A فرق الطاقة بين المستويات F = I ±1/2 في حقل معدوم).
وبالتالي تكتب العلاقة (علاقة Breit-Rabi):
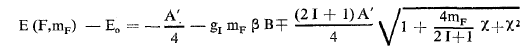
الإشارة موجبة مطابقة للحالة F = I +1/2 والإشارة سالبة من أجل F = I -1/2، عندما يكون الحقل المغناطيسي ضعيف (1 > χ) وعندما يكون قوي (1<χ) وإشارة ± المختارة هي إشارة العدد الكمي mJ، تسمح هذه العلاقات بإقامة الحسابات العددية لمخططات زيمان، والشكل (1) يعطي أمثلة على ذلك.
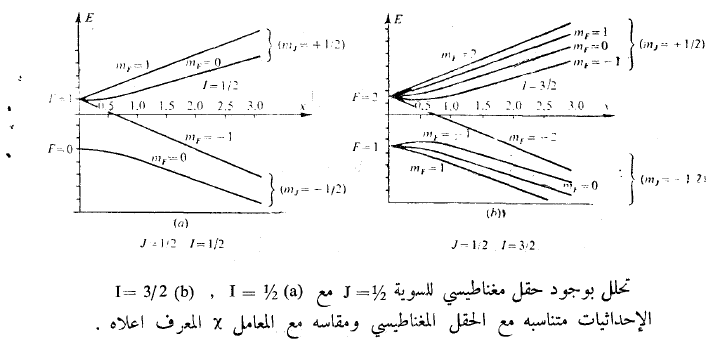
شكل (1)
الاكثر قراءة في الفيزياء الذرية
اخر الاخبار
اخبار العتبة العباسية المقدسة
