
خصائص الجسيمات الأولية: الزخم الزاوي البرمي Spin
 المؤلف:
سعد ناجي عبود
المؤلف:
سعد ناجي عبود
 المصدر:
مقدمة في فيزياء الطاقة العالية والاشعاع الكوني
المصدر:
مقدمة في فيزياء الطاقة العالية والاشعاع الكوني
 الجزء والصفحة:
ص19–21
الجزء والصفحة:
ص19–21
 2023-11-13
2023-11-13
 1934
1934
فكرة الزخم الزاوي البرمي تعود إلى عام 1926 عندما افترض يولنبنك وکاود سميث في محاولتهما لتفسير التركيب الدقيق لخطوط الأطياف الذرية (fine structure)، بأن الإلكترون يدور حول محوره كملا تفعل الأرض وبذا يمتلك زخما زاويا برميا (→s) Spin وقد امتدت هذه الفكرة فشملت كل الجسيمات. أن زخم الجسيمة يساوي زخم ضديدها بالمقدار لكنهما يختلفان عن بعضهما باتجاه الدوران حول محوريهما. ويقدر الزخم البرمي بوحدات πh/2 = .ħوتقسم الجسيمات من حيث زخمها إلى قسمين وهما:
أولا: الفيرميونات Fermions
وهي جسيمات زخمها الزاوي البرمي عددا فرديا مضروبا في 1/2 أي أن 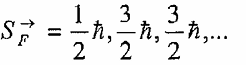 ، وتشمل هذه الجسيمات الباريونات واللبتونات مثلا:
، وتشمل هذه الجسيمات الباريونات واللبتونات مثلا: 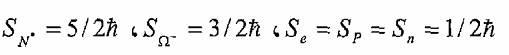 ، والفيرميونات تخضع لمبدأ الاستثناء لباولي (Pauli exclusion principle) والذي ينص على أنه لا يمكن لفيرميونين (إلكترونين، بروتونين) أن يتواجدا بنفس الحالة الكمية وتكون لهما نفس أعداد الكم الأربعة (s، ml، l، n). كما وإنها تخضع لقانون التوزيع لفيرمي – ديراك Fermi–Dirac distribution law)) ولهذا سميت بالفيرميونات.
، والفيرميونات تخضع لمبدأ الاستثناء لباولي (Pauli exclusion principle) والذي ينص على أنه لا يمكن لفيرميونين (إلكترونين، بروتونين) أن يتواجدا بنفس الحالة الكمية وتكون لهما نفس أعداد الكم الأربعة (s، ml، l، n). كما وإنها تخضع لقانون التوزيع لفيرمي – ديراك Fermi–Dirac distribution law)) ولهذا سميت بالفيرميونات.
ثانيا: البوزونات Bosons
جسيمات زخمها الزاوي البرمي يساوي عدد صحيح 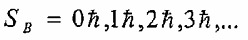 من هذه الجسيمات الفوتون ħ1 = Sr، والبايونات ħ0 = πS والكايونات ħ0 = SK والكرافيتون ħ2 = Sg والبوزونات لا تخضع لمبدأ الاستثناء لباولي ولهذا يمكن وجود أي عدد منها في نفس الحالة الكمية كما في حالة وجود عدد غير محدد من البايونات محيطة بالبروتون أو النيوترون مثلا. وهي تخضع لقانون التوزيع لبوز – أينشتين (Bose–Einstein distribution law) ولهذا سميت بالبوزونات، ويبدوا أن الجسيمة بسبب زخمها الزاوي البرمي تمتلك عزما مغناطيسيا، فعندما توضع في مجال مغناطيسي فأن زخمها سيتجه باتجاهات معينة وعددها (عدد الأوضاع التي تتخذها الجسيمة في المجال المغناطيسي 1 + s2). ففي حالة الإلكترون الذي زخمه ħs=1/2 هناك اتجاهان أو وضعان يمكن أن يأخذها الإلكترون بالنسبة للمجال المغناطيسي هما الأول: وفيه يكون اتجاه الزخم بنفس اتجاه المجال والثاني: وفيه اتجاه الزخم معاكس لاتجاه المجال. ويشار لهاتين الحالتين بمركبة الزخم الزاوي البرمي على اتجاه المجال بالرمز ms (العدد الكمي المغناطيسي البرميspin magnetic quantum number). وقيم ms للإلكترون هما
من هذه الجسيمات الفوتون ħ1 = Sr، والبايونات ħ0 = πS والكايونات ħ0 = SK والكرافيتون ħ2 = Sg والبوزونات لا تخضع لمبدأ الاستثناء لباولي ولهذا يمكن وجود أي عدد منها في نفس الحالة الكمية كما في حالة وجود عدد غير محدد من البايونات محيطة بالبروتون أو النيوترون مثلا. وهي تخضع لقانون التوزيع لبوز – أينشتين (Bose–Einstein distribution law) ولهذا سميت بالبوزونات، ويبدوا أن الجسيمة بسبب زخمها الزاوي البرمي تمتلك عزما مغناطيسيا، فعندما توضع في مجال مغناطيسي فأن زخمها سيتجه باتجاهات معينة وعددها (عدد الأوضاع التي تتخذها الجسيمة في المجال المغناطيسي 1 + s2). ففي حالة الإلكترون الذي زخمه ħs=1/2 هناك اتجاهان أو وضعان يمكن أن يأخذها الإلكترون بالنسبة للمجال المغناطيسي هما الأول: وفيه يكون اتجاه الزخم بنفس اتجاه المجال والثاني: وفيه اتجاه الزخم معاكس لاتجاه المجال. ويشار لهاتين الحالتين بمركبة الزخم الزاوي البرمي على اتجاه المجال بالرمز ms (العدد الكمي المغناطيسي البرميspin magnetic quantum number). وقيم ms للإلكترون هما
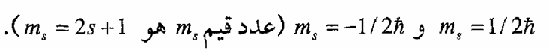
 الاكثر قراءة في فيزياء الجسيمات
الاكثر قراءة في فيزياء الجسيمات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


