
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الكواركات Quarks
المؤلف:
سعد ناجي عبود
المصدر:
مقدمة في فيزياء الطاقة العالية والاشعاع الكوني
الجزء والصفحة:
ص47–52
2023-11-14
1076
بعد نجاح فكرة الزخم الأيزوباري، حيث رتبت الجسيمات في مجاميع أحادية وثنائية وثلاثية، وبعد ازدياد عدد الجسيمات بذلت محاولات عديدة لتصنيف وتجميع هذه الجسيمات. ومن هذه المحاولات طريقة كلمان الثمانية Gellmann eight fold way والتي تسمى أيضا نظرية (3)SU. ومن توقعات هذه النظرية أمكانية ترتيب الميزونات والباريونات في مجاميع أحادية، ثمانية وعشرية. ولقد تم فعلا الحصول على مثل هذه المجاميع وذلك برسم مجموع الغرابة والعدد الباريوني والذي يسمى بالشحنة الفوقية (Y=S+B (hypercharge كدالة للزخم الأيزوباري T3. ومن أبرز نجاحات هذه النظرية التنبؤ بوجود جسيمة أسماها كلمان جسيمة –Ω والتي تتصف بشحنة سالبة وغرابة –3 = S و0 = T = T3 وكتلتها تساوي 5MeV 167 
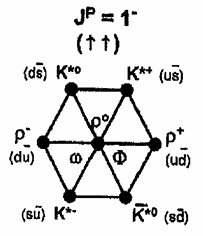
الشكل (1–3) المثمن الميزوني عند –1 = J
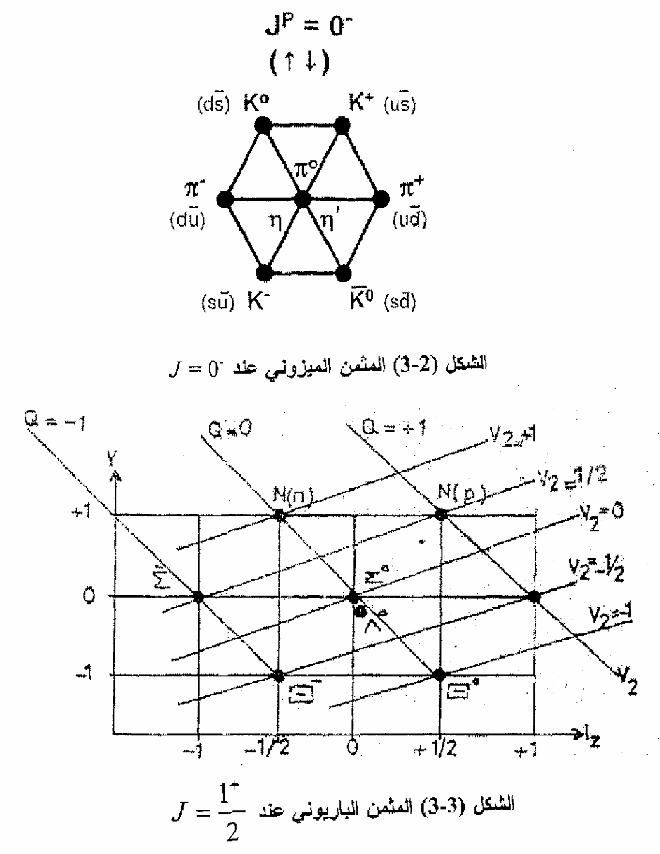
من الشكل (3–3) نلاحظ ما يأتي:
1– البروتون والنيوترون ينتميان إلى نفس النظائر المزدوجة (مجموعة ثنائية أيزوبارية) لها 1 = T والمركبة الثالثة 1/2 = T3 للبروتون و -1/2 = T3 للنيوترون.
2– جسيمة سكما ∑ هي ثلاثية النظائر وجسيمة كساي 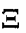 هي ثنائية النظائر.
هي ثنائية النظائر.
3– الجسيمات التي تقع على نفس الخط الأفقي تكون النظائر المتعددة والمتشابهة.
4– جميع الجسيمات الموجودة في الشكل لها برم 1/2 = S وتناظر موجب. لذا فأن أسمها في بعض الأحيان يطلق عليه +1/2 = S الثمانية (1/2+ = Octet J).
لحد الآن لن نرى شيئا جديدا. لكن عند تغيرنا للمحاور بحيث نجمع جسيمة البروتون P مع جسيمة سكما +∑ والتي هي على نفس الخط المائل فنحن نستطيع القول بأنها تكون مجموعة جديدة لها مظهران بنفس القاعدة. أذن سوف نقدم عددا كميا مشابه إلى البوم الأيزوباري والذي هو البرم الموحد (Unitary spin). وبذلك نقول بأن P++∑ تشكل الزوج الموحد (Unitary doublet) وبقيمة إلى U مساوية إلى 1/2. هناك قيمتان إلى: الأولى 1/2+ = Uz وهذه للبروتون أما الثانية فهي 1/2- = Uz وهذه إلى +∑ وهكذا لبقية الجسيمات.
أما الخط المائل الأسفل فهو يمر في 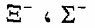 وهذه أيضا تمثل الزوج الموحد مع
وهذه أيضا تمثل الزوج الموحد مع 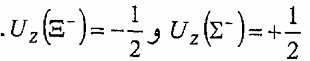
وأخيرا الخط المائل في الوسط، فيمر بثلاث جسيمات هي النيوترون و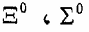 لذا فهو ثلاثي مع 1 = Uz وأن
لذا فهو ثلاثي مع 1 = Uz وأن 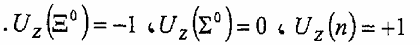 ومن الملاحظ في الشكل أن الجسيمات الواقعة على نفس الخط المائل لها نفس الشحنة. كذلك فأن:
ومن الملاحظ في الشكل أن الجسيمات الواقعة على نفس الخط المائل لها نفس الشحنة. كذلك فأن:

وهذه النظرية للانفصال، تعتمد على U والتي هي عامل جديد لنظرية (3)SU
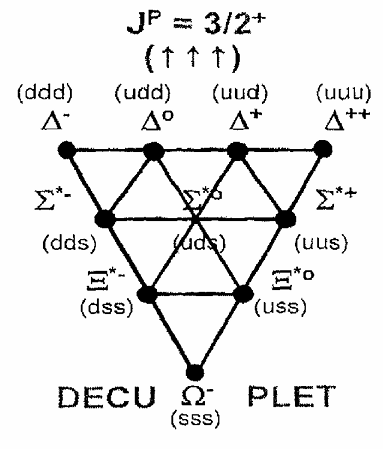
الشكل (4–3) المعشر الباريوني عند J = +3/2
الآن لنرى أهمية نظرية (3) SU. قلنا أن الباريونات تمثل ثماني حالات لجسيمات لها JP = +1/2. وللميزونات هناك أيضا ثماني حالات لجسيمات أخرى لها -0 = JP. وإذا افترضنا أن هذه الجسيمات ترتبط مع بعضها وبذلك يكون هنالك 64 حالة مختلفة هذه الأربع والستون حالة تتجمع في مجاميع (1,8,8,10,10,27). مثلا ضرب الباريونات الثمانية مع نفسها سوف يعطينا كل الحالات المستقرة وغير المستقرة المتكونة من باريونين.
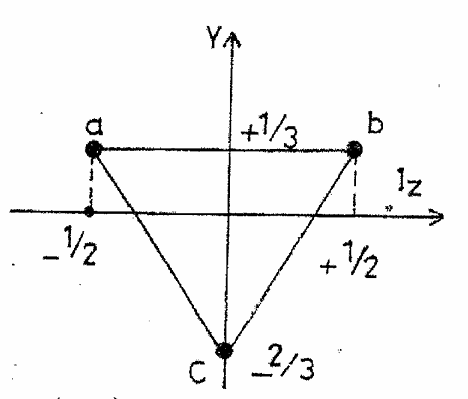
الشكل (5–3) مجموعة A متكونة من ثلاثة أعضاء A = (a, b, c)
لنفرض أن المجموعة A متكونة من ثلاثة أعضاء (a, b, c) يمكن تمثيلها بالمثلث الذي رأسه إلى الأسفل (الشكل (5–3)) وبدالة (3). المجموعة الثانية إلى A هي –A (A المضادة) حيث تتكون من ثلاثة أعضاء مضادين للمجموعة الأولى وهم –, a–, b–,c ويمكننا تمثيلها بمثلث رأسه إلى الأعلى (الشكل (6–3)) وبدالة (–3)، ويربط أعضاء المثلثين مع بعض تنتج مجموعة تمثل بالدالة (–3) x (3) وتشمل تسع أعضاء. ومن الممكن كتابة هذه المجموعة من ثمانية أعضاء زائدا واحد وكما يأتي:
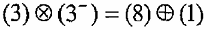
أما في حالة ضرب مجموعتين من ثمانية أعضاء فنحصل على أربعة وستين عضوا وكما يلي:
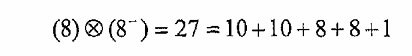

الشكل (6–3) مجموعة متكونة من ثلاثة اعضاء (A = (a-, b-, c-