
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Fermat’s principle of least time
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 26
2024-03-16
1882
Now in the further development of science, we want more than just a formula. First, we have an observation, then we have numbers that we measure, then we have a law which summarizes all the numbers. But the real glory of science is that we can find a way of thinking such that the law is evident.
The first way of thinking that made the law about the behavior of light evident was discovered by Fermat in about 1650, and it is called the principle of least time, or Fermat’s principle. His idea is this: that out of all possible paths that it might take to get from one point to another, light takes the path which requires the shortest time.
Let us first show that this is true for the case of the mirror, that this simple principle contains both the law of straight-line propagation and the law for the mirror. So, we are growing in our understanding! Let us try to find the solution to the following problem. In Fig. 26–3 is shown two points, A and B, and a plane mirror, MM′. What is the way to get from A to B in the shortest time? The answer is to go straight from A to B! But if we add the extra rule that the light has to strike the mirror and come back in the shortest time, the answer is not so easy. One way would be to go as quickly as possible to the mirror and then go to B, on the path ADB. Of course, we then have a long path DB. If we move over a little to the right, to E, we slightly increase the first distance, but we greatly decrease the second one, and so the total path length, and therefore the travel time, is less. How can we find the point C for which the time is the shortest? We can find it very nicely by a geometrical trick.
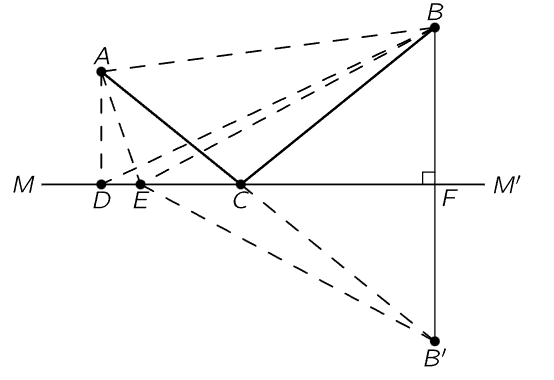
Fig. 26–3. Illustration of the principle of least time.
We construct on the other side of MM′ an artificial point B′, which is the same distance below the plane MM′ as the point B is above the plane. Then we draw the line EB′. Now because BFM is a right angle and BF=FB′, EB is equal to EB′. Therefore, the sum of the two distances, AE+EB, which is proportional to the time it will take if the light travels with constant velocity, is also the sum of the two lengths AE+EB′. Therefore, the problem becomes, when is the sum of these two lengths the least? The answer is easy: when the line goes through point C as a straight line from A to B′! In other words, we have to find the point where we go toward the artificial point, and that will be the correct one. Now if ACB′ is a straight line, then angle BCF is equal to angle B′CF and thence to angle ACM. Thus the statement that the angle of incidence equals the angle of reflection is equivalent to the statement that the light goes to the mirror in such a way that it comes back to the point B in the least possible time. Originally, the statement was made by Hero of Alexandria that the light travels in such a way that it goes to the mirror and to the other point in the shortest possible distance, so it is not a modern theory. It was this that inspired Fermat to suggest to himself that perhaps refraction operated on a similar basis. But for refraction, light obviously does not use the path of shortest distance, so Fermat tried the idea that it takes the shortest time.
Before we go on to analyze refraction, we should make one more remark about the mirror. If we have a source of light at the point B and it sends light toward the mirror, then we see that the light which goes to A from the point B comes to A in exactly the same manner as it would have come to A if there were an object at B′, and no mirror. Now of course the eye detects only the light which enters it physically, so if we have an object at B and a mirror which makes the light come into the eye in exactly the same manner as it would have come into the eye if the object were at B′, then the eye-brain system interprets that, assuming it does not know too much, as being an object at B′. So the illusion that there is an object behind the mirror is merely due to the fact that the light which is entering the eye is entering in exactly the same manner, physically, as it would have entered had there been an object back there (except for the dirt on the mirror, and our knowledge of the existence of the mirror, and so on, which is corrected in the brain).
Now let us demonstrate that the principle of least time will give Snell’s law of refraction. We must, however, make an assumption about the speed of light in water. We shall assume that the speed of light in water is lower than the speed of light in air by a certain factor, n.
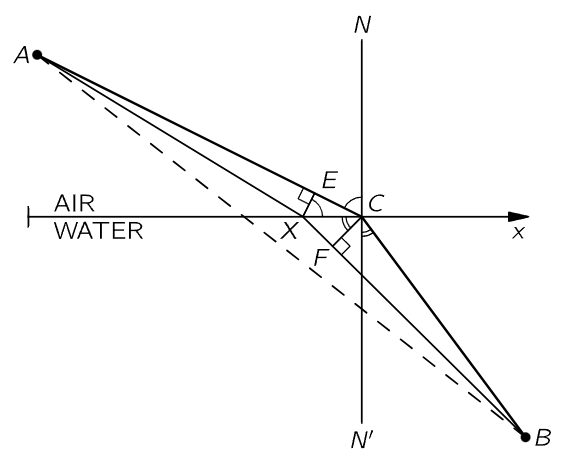
Fig. 26–4. Illustration of Fermat’s principle for refraction.
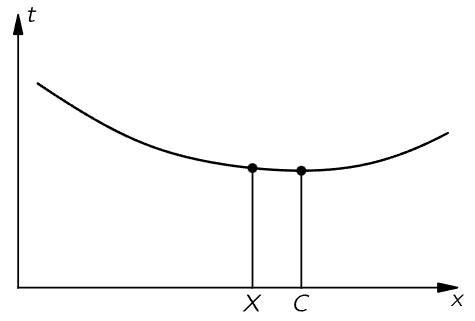
Fig. 26–5. The minimum time corresponds to point C, but nearby points correspond to nearly the same time.
In Fig. 26–4, our problem is again to go from A to B in the shortest time. To illustrate that the best thing to do is not just to go in a straight line, let us imagine that a beautiful girl has fallen out of a boat, and she is screaming for help in the water at point B. The line marked x is the shoreline. We are at point A on land, and we see the accident, and we can run and can also swim. But we can run faster than we can swim. What do we do? Do we go in a straight line? (Yes, no doubt!) However, by using a little more intelligence we would realize that it would be advantageous to travel a little greater distance on land in order to decrease the distance in the water, because we go so much slower in the water. (Following this line of reasoning out, we would say the right thing to do is to compute very carefully what should be done!) At any rate, let us try to show that the final solution to the problem is the path ACB, and that this path takes the shortest time of all possible ones. If it is the shortest path, that means that if we take any other, it will be longer. So, if we were to plot the time it takes against the position of point X, we would get a curve something like that shown in Fig. 26–5, where point C corresponds to the shortest of all possible times. This means that if we move the point X to points near C, in the first approximation there is essentially no change in time because the slope is zero at the bottom of the curve. So, our way of finding the law will be to consider that we move the place by a very small amount, and to demand that there be essentially no change in time. (Of course, there is an infinitesimal change of a second order; we ought to have a positive increase for displacements in either direction from C.) So we consider a nearby point X and we calculate how long it would take to go from A to B by the two paths, and compare the new path with the old path. It is very easy to do. We want the difference, of course, to be nearly zero if the distance XC is short. First, look at the path on land. If we draw a perpendicular XE, we see that this path is shortened by the amount EC. Let us say we gain by not having to go that extra distance. On the other hand, in the water, by drawing a corresponding perpendicular, CF, we find that we have to go the extra distance XF, and that is what we lose. Or, in time, we gain the time it would have taken to go the distance EC, but we lose the time it would have taken to go the distance XF. Those times must be equal since, in the first approximation, there is to be no change in time. But supposing that in the water the speed is 1/n times as fast as in air, then we must have

Therefore we see that when we have the right point, XC sin EXC=n⋅XC sin XCF or, cancelling the common hypotenuse length XC and noting that
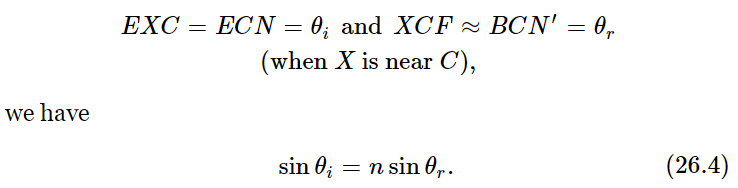
So we see that to get from one point to another in the least time when the ratio of speeds is n, the light should enter at such an angle that the ratio of the sines of the angles θi and θr is the ratio of the speeds in the two media.
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















