
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Diffraction of light by a screen
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 31
2024-03-23
1823
It is now a good time to take up a somewhat different matter which we can handle with the machinery of this chapter. In the last chapter we said that when you have an opaque screen and the light can come through some holes, the distribution of intensity—the diffraction pattern—could be obtained by imagining instead that the holes are replaced by sources (oscillators) uniformly distributed over the hole. In other words, the diffracted wave is the same as though the hole were a new source. We have to explain the reason for that, because the hole is, of course, just where there are no sources, where there are no accelerating charges.
Let us first ask: “What is an opaque screen?” Suppose we have a completely opaque screen between a source S and an observer at P, as in Fig. 31–6(a). If the screen is “opaque” there is no field at P. Why is there no field there? According to the basic principles we should obtain the field at P as the field Es of the source delayed, plus the field from all the other charges around. But, as we have seen above, the charges in the screen will be set in motion by the field Es, and these motions generate a new field which, if the screen is opaque, must exactly cancel the field Es on the back side of the screen. You say: “What a miracle that it balances exactly! Suppose it was not exactly right!” If it were not exactly right (remember that this opaque screen has some thickness), the field toward the rear part of the screen would not be exactly zero. So, not being zero, it would set into motion some other charges in the material of the screen, and thus make a little more field, trying to get the total balanced out. So, if we make the screen thick enough, there is no residual field, because there is enough opportunity to finally get the thing quieted down. In terms of our formulas above we would say that the screen has a large and imaginary index, so the wave is absorbed exponentially as it goes through. You know, of course, that a thin enough sheet of the opaquest material, even gold, is transparent.
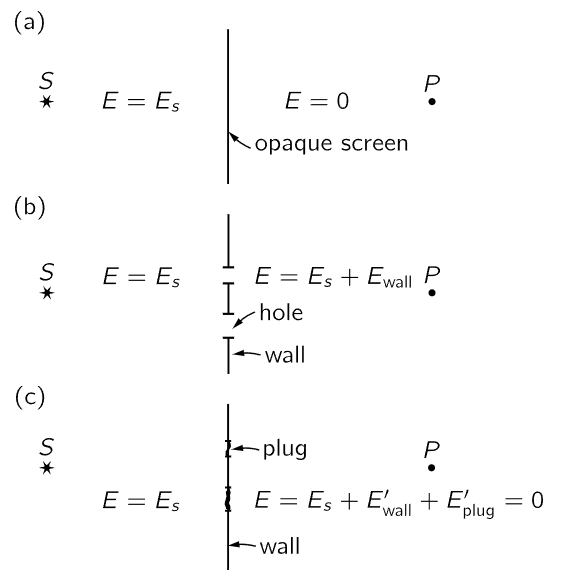
Fig. 31–6. Diffraction by a screen.
Now let us see what happens with an opaque screen which has holes in it, as in Fig. 31–6(b). What do we expect for the field at P? The field at P can be represented as a sum of two parts—the field due to the source S plus the field due to the wall, i.e., due to the motions of the charges in the walls. We might expect the motions of the charges in the walls to be complicated, but we can find out what fields they produce in a rather simple way.
Suppose that we were to take the same screen, but plug up the holes, as indicated in part (c) of the figure. We imagine that the plugs are of exactly the same material as the wall. Mind you, the plugs go where the holes were in case (b). Now let us calculate the field at P. The field at P is certainly zero in case (c), but it is also equal to the field from the source plus the field due to all the motions of the atoms in the walls and in the plugs. We can write the following equations:
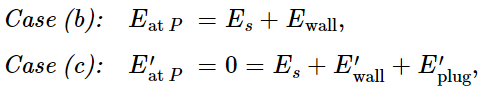
where the primes refer to the case where the plugs are in place, but Es is, of course, the same in both cases. Now if we subtract the two equations, we get
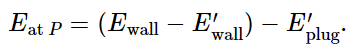
Now if the holes are not too small (say many wavelengths across), we would not expect the presence of the plugs to change the fields which arrive at the walls except possibly for a little bit around the edges of the holes. Neglecting this small effect, we can set Ewall=E′wall and obtain that
Eat P = −E′plug.
We have the result that the field at P when there are holes in a screen (case b) is the same (except for sign) as the field that is produced by that part of a complete opaque wall which is located where the holes are! (The sign is not too interesting, since we are usually interested in intensity which is proportional to the square of the field.) It seems like an amazing backwards-forwards argument. It is, however, not only true (approximately for not too small holes), but useful, and is the justification for the usual theory of diffraction.
The field E′plug is computed in any particular case by remembering that the motion of the charges everywhere in the screen is just that which will cancel out the field Es on the back of the screen. Once we know these motions, we add the radiation fields at P due just to the charges in the plugs.
We remark again that this theory of diffraction is only approximate, and will be good only if the holes are not too small. For holes which are too small the E′plug term will be small and then the difference between E′wall and Ewall (which difference we have taken to be zero) may be comparable to or larger than the small E′plug term, and our approximation will no longer be valid.
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















