
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
PHASE MATCHING
المؤلف:
Mark Csele
المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
الجزء والصفحة:
p223
21-3-2016
3875
PHASE MATCHING
The three terms that result are plotted in Figure 1.1 and summed together. The ⍵ and 2⍵ terms are in-phase and add together to form a] sine wave, but when all three terms are added together, the result (the total polarization) is a warped wave, shown in Figure 1.1. The peaks and valleys of the summed wave still coincide with those of the original incident wave (i.e., it is in phase with the original ⍵ term), but the wave is shifted in one direction in this case, upward. This is possible only if the nonlinear crystal has no internal symmetry, so that electron shells are relocated more effectively in one direction than in the other by the electric field applied. About 10% of all crystals have such a lack of symmetry and hence can be used as nonlinear media.
Now, considering that there are two frequencies of light in the crystal, it is quite likely that each will have a slightly different index of refraction. This effect, of course, is responsible for dispersion of light of various wavelengths by a prism. In most crystals the index of refraction will be higher for the higher-frequency component (2⍵) than for the lower-frequency component. A higher index of refraction means that light travels more slowly. Figure 1.2 illustrates the situation in which the second harmonic light becomes out of phase with the fundamental component as
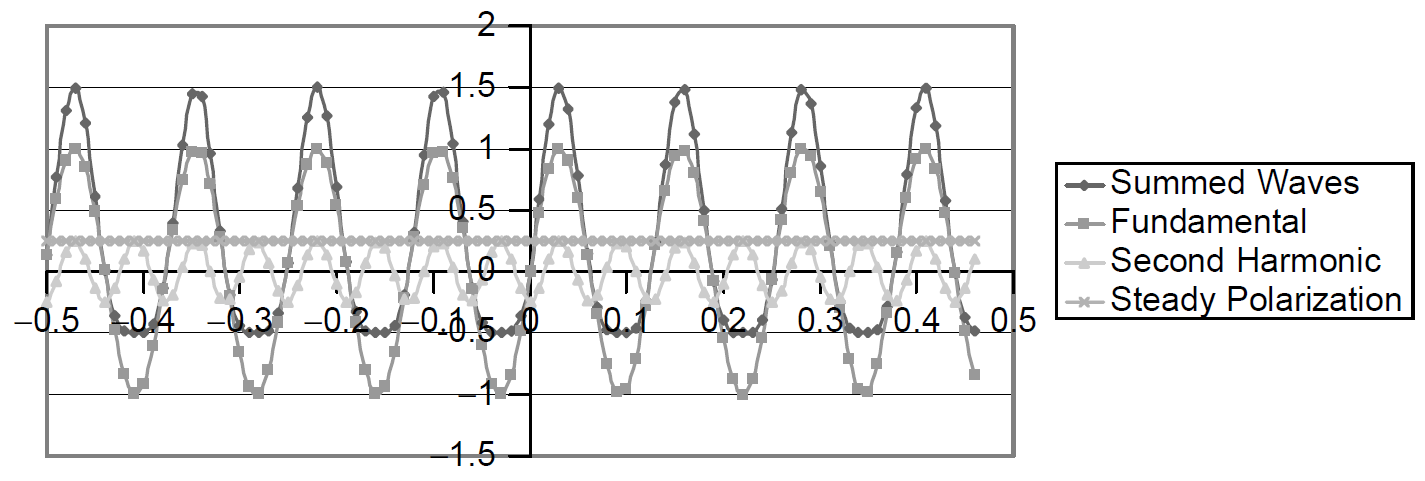
Figure 1.1. Output terms.
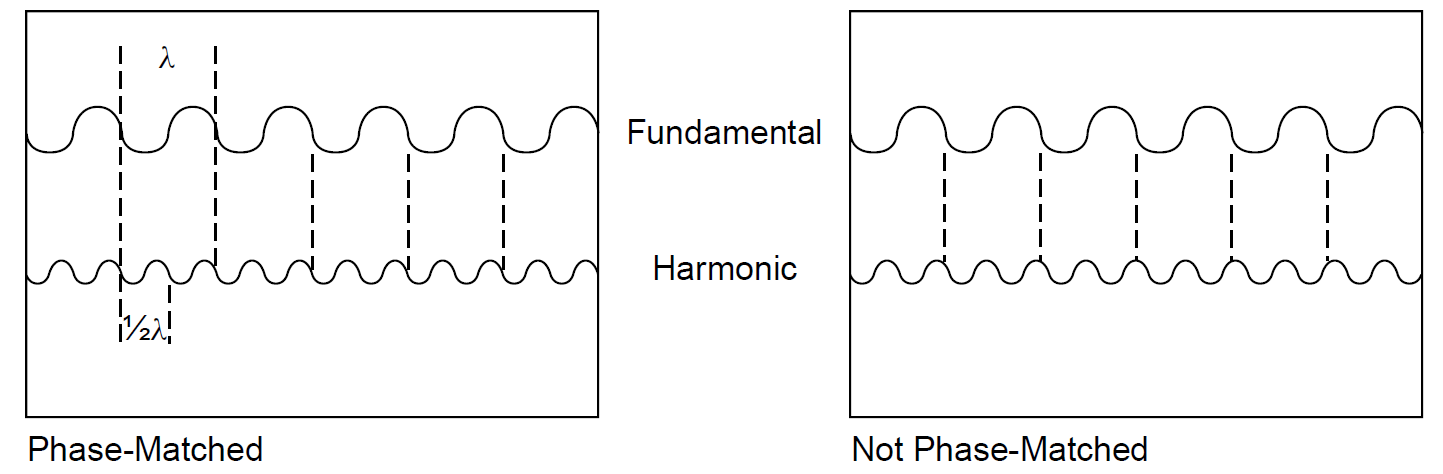
Figure 1.2. Phase shift of components in a nonlinear crystal.
it passes through the crystal, causing destructive interference, which leads to extinction of the second harmonic component. The distance over which the waves travel before becoming 1808 out of phase is called the coherence length. If the crystal is thinner than this length (typically, 10-3 cm or less), the components remain in phase. This is somewhat impractical, though, and severely limits the efficiency of the harmonic light generation. If, the crystal is thicker and happens to have a thickness that is an odd multiple of the coherence length, the generated second harmonic light is entirely extinguished, due to destructive interference.
The solution to the problem of phase mismatch between the components is to exploit the phenomenon of birefringence. That this is an effect in which the index of refraction depends on the polarization of light passing through the crystal, or in this case, the individual light component passing through the crystal. By tilting the crystal such that the index of refraction for both the fundamental (with one specific polarization) and the harmonic component (with a different polarization) are the same, phase matching can be accomplished. When the direction of propagation of light in the crystal is chosen so that the indexes of refraction for both the fundamental and second harmonic are exactly the same, the crystal is said to be phase matched. The second harmonic component produced in the crystal now exits in phase with the fundamental component, so that constructive interference occurs. This has implications for efficiency of generation of second harmonic light.
Nonlinear interaction is a general term describing the mixing of two light beams to produce a sum or difference of frequencies. The case of second-harmonic generation, the most common application of nonlinear phenomena, is a specific case in which the input components are identical (with the same frequency) and interact to produce a resulting beam with a doubled frequency. Other interactions are possible, of course, such as the mixing of a fundamental and second-harmonic beam to produce third-harmonic output, the most common application being the mixing of a 1064-nm fundamental from a YAG laser with a 532-nm frequency doubled beam to produce a third-harmonic output at 355 nm.
Nonlinear crystals are classified by the type of phase matching required, each type requiring a different polarization of each input component. Type I phase matched crystals utilize input beams with polarizations parallel to each other, while type II phase-matched crystals utilize input beams with polarizations perpendicular to each other. Both types of crystals are outlined in Figure 1.3, in which input components ⍵1 and ⍵2 (identical for a second-harmonic generator) are mixed to produce an output at frequency ⍵3. As an example of phase matching, consider a small green DPSS laser in which vanadate (a common solid-state laser crystal normally with an output at 1064 nm in the infrared) is frequency-doubled to produce green light at 532 nm using a type II phase-matched crystal of KTP (a common nonlinear crystal). Vanadate produces a polarized output at 1064 nm that is oriented at 45 degrees to the optical axis of the KTP crystal. This output is hence split into two polarization components (the o and e components) perpendicular to each other, as required for type II phase matching. A second-harmonic beam is generated with a rotation of 45 degrees relative to the 1064-nm output from the vanadate, which exits through the output coupler. The optical train of such a laser is described in Figure 1.4 along with relative polarizations of each component.
Many commercial frequency-doubling crystals, especially those intended for use in compact DPSS lasers, are cut specifically with the faces perpendicular to the optical axis of the laser and such that the crystal may be oriented in the same direction as the lasing crystal. In this manner, the user is generally not aware of the requirement for phase matching, and the crystal is simply installed in the same orientation as the solid state laser crystal. For a crystal with unknown axes, phase matching can be accomplished by mounting the crystal in a mount allowing angular adjustment, and passing the beam from a Q-switched laser through the crystal (a Q-switched laser is used since the peak intensities are extremely high, as required for high second-harmonic generation efficiency). By rotating the crystal while the beam from the laser passes through it, second-harmonic light will be generated when the phase-matching angle is encountered. The angle may then be optimized for peak second-harmonic output, at which point the phase-matching direction has been found. The crystal may also be inserted into the cavity of a laser and adjusted as well.
The scheme outlined in Figure 1.4 may seem somewhat cumbersome. After all, why not simply frequency-double the diode output directly by placing the nonlinear
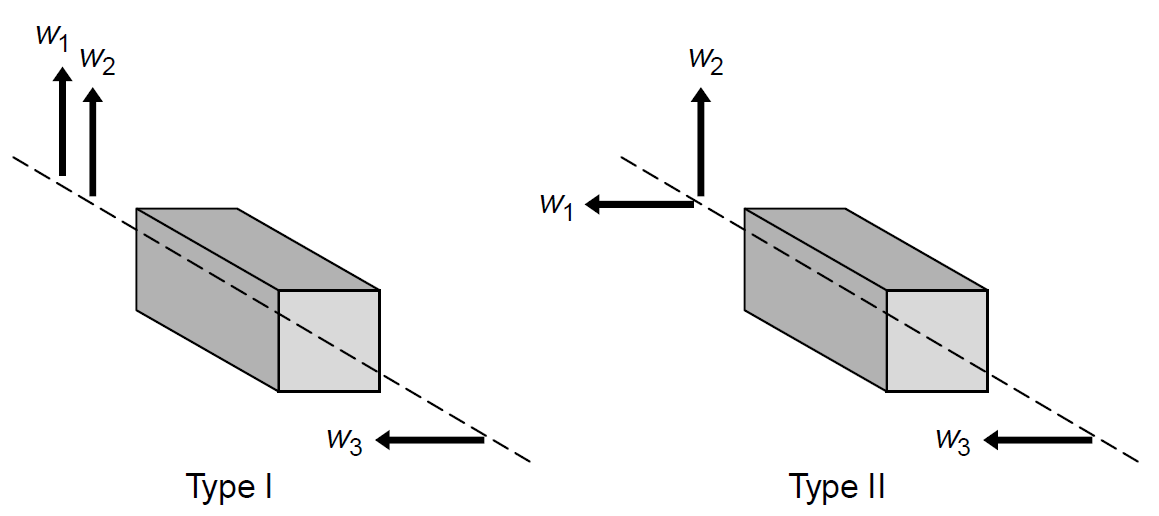
Figure 1.3. Types of phase matching.

Figure 1.4. Type II phase matching in a DPSS laser.
crystal inside the cavity of the laser? With a normal laser diode, this is not possible because the relatively wide gain bandwidth of most diodes prevents proper phase matching at all but one specific wavelength. However, inclusion of a wave length selective element such as a Bragg reflector in the cavity narrows the spectral width, allowing efficient harmonic generation. Other approaches include the optical pumping of a semiconductor laser (as opposed to a normal solid-state laser crystal) with a nonlinear doubling crystal inside the cavity. Solid-state lasers such as the YAG, on the other hand, feature much narrower gain bandwidths, so are already ideally suited for doubling. In addition to angular adjustment, phase matching of some nonlinear crystals may be achieved by changing the temperature of the crystal itself. Such crystals exhibit indexes of refraction that change with temperature. Niobates such as lithium niobate (LiNbO3) exhibit such behavior (which was discovered by accident when it was evident that the phase-matching direction of this material was different for various temperatures). For these materials the crystal is placed inside an oven, and the temperature varied until phase matching occurs in a manner similar to that employed for angular phase matching. This method is used to tune most parametric oscillators, described later in the chapter.
It is obvious that phase matching is essential for high conversion efficiency, which also depends on the nonlinear coefficient of the material and the intensity of the laser beam (hence, as we mentioned earlier, why harmonic generators are often placed inside the cavity of a laser where the intensity is very high). Efficiency of conversion can be as high as 70% but normally hovers around 30% for a material such as KDP.
An alternative method to ensure phase matching is quasi-phase matching using a periodically poled nonlinear material. In such a material, thin layers of nonlinear material are stacked with polarizations in opposite directions. As the fundamental and harmonic waves both propagate as they pass through the crystal, phase shifts occur due to the differing refractive indexes at each wavelength. By reversing the phase mismatch periodically, phase matching can be accomplished without the use of angular rotation (which exploits birefringence). Such crystals offer wider wavelength ranges since they operate independently of the wavelength range over which birefringence can be exploited. Production of such crystals is a complex process, however, so the cost is high compared with that of standard birefringent crystals.
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















