


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-7-2018
Date: 12-6-2018
Date: 24-5-2018
|
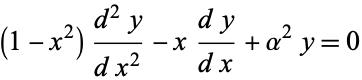 |
(1) |
for 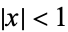 . The Chebyshev differential equation has regular singular points at
. The Chebyshev differential equation has regular singular points at 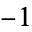 , 1, and
, 1, and 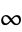 . It can be solved by series solution using the expansions
. It can be solved by series solution using the expansions
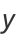 |
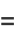 |
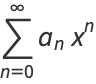 |
(2) |
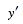 |
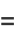 |
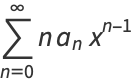 |
(3) |
 |
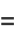 |
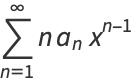 |
(4) |
 |
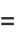 |
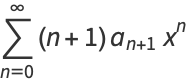 |
(5) |
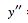 |
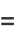 |
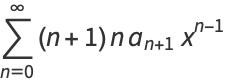 |
(6) |
 |
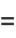 |
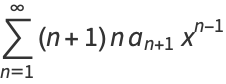 |
(7) |
 |
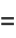 |
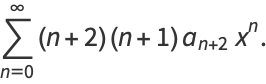 |
(8) |
Now, plug equations (6) and (8) into the original equation (◇) to obtain
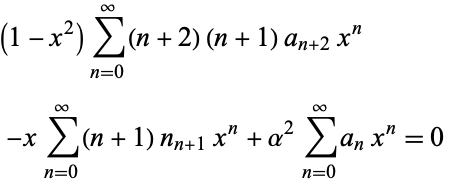 |
(9) |
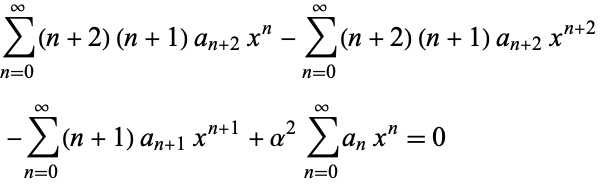 |
(10) |
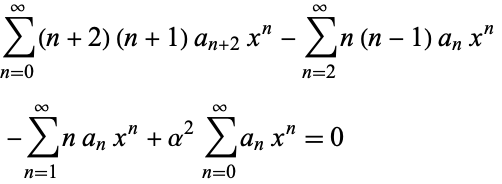 |
(11) |
![2·1a_2+3·2a_3x-1·ax+alpha^2a_0+alpha^2a_1x
+sum_(n=2)^infty[(n+2)(n+1)a_(n+2)-n(n-1)a_n-na_n+alpha^2a_n]x^n=0](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/NumberedEquation5.gif) |
(12) |
![(2a_2+alpha^2a_0)+[(alpha^2-1)a_1+6a_3]x
+sum_(n=2)^infty[(n+2)(n+1)a_(n+2)+(alpha^2-n^2)a_n]x^n=0,](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/NumberedEquation6.gif) |
(13) |
so
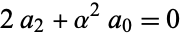 |
(14) |
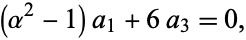 |
(15) |
and by induction,
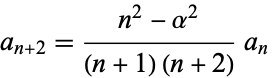 |
(16) |
for 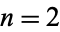 , 3, ....
, 3, ....
Since (14) and (15) are special cases of (16), the general recurrence relation can be written
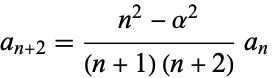 |
(17) |
for 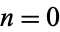 , 1, .... From this, we obtain for the even coefficients
, 1, .... From this, we obtain for the even coefficients
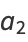 |
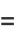 |
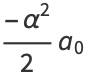 |
(18) |
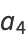 |
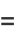 |
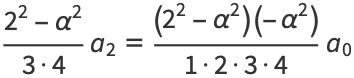 |
(19) |
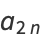 |
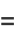 |
![([(2n)^2-alpha^2][(2n-2)^2-alpha^2]...(-alpha^2))/((2n)!)a_0,](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/Inline35.gif) |
(20) |
and for the odd coefficients
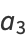 |
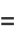 |
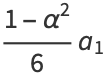 |
(21) |
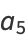 |
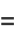 |
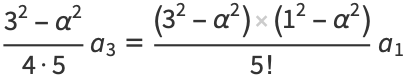 |
(22) |
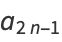 |
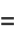 |
![([(2n-1)^2-alpha^2][(2n-3)^2-alpha^2]...[1^2-alpha^2])/((2n+1)!)a_1.](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/Inline44.gif) |
(23) |
The even coefficients 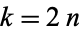 can be given in closed form as
can be given in closed form as
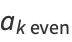 |
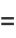 |
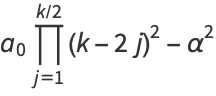 |
(24) |
 |
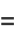 |
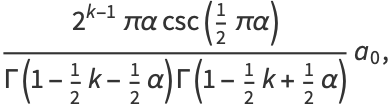 |
(25) |
and the odd coefficients 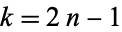 as
as
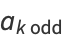 |
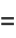 |
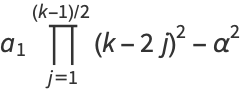 |
(26) |
 |
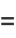 |
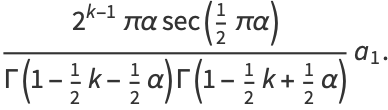 |
(27) |
The general solution is then given by summing over all indices,
![y=a_0[1+sum_(k=2,4,...)^infty(a_(k even))/(k!)x^k]
+[x+sum_(k=3,5,...)^infty(a_(k odd))/(k!)x^k],](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/NumberedEquation11.gif) |
(28) |
which can be done in closed form as
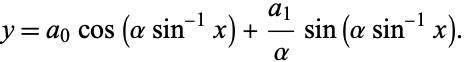 |
(29) |
Performing a change of variables gives the equivalent form of the solution
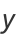 |
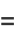 |
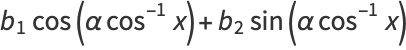 |
(30) |
 |
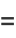 |
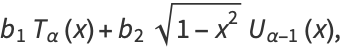 |
(31) |
where 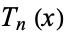 is a Chebyshev polynomial of the first kind and
is a Chebyshev polynomial of the first kind and 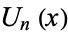 is a Chebyshev polynomial of the second kind. Another equivalent form of the solution is given by
is a Chebyshev polynomial of the second kind. Another equivalent form of the solution is given by
![y=c_1cosh[alphaln(x+sqrt(x^2-1))]
+ic_2sinh[alphaln(x+sqrt(x^2-1))].](http://mathworld.wolfram.com/images/equations/ChebyshevDifferentialEquation/NumberedEquation13.gif) |
(32 |
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 735, 1985.
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed. New York: Wiley, pp. 232 and 252, 1986.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 127, 1997.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
في مدينة الهرمل اللبنانية.. وفد العتبة الحسينية المقدسة يستمر بإغاثة العوائل السورية المنكوبة
|
|
|