


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-8-2019
Date: 9-6-2019
Date: 24-6-2019
|
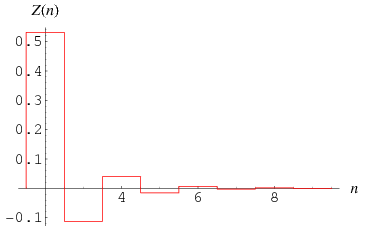
Define the Airy zeta function for 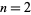 , 3, ... by
, 3, ... by
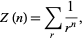 |
(1) |
where the sum is over the real (negative) zeros 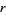 of the Airy function
of the Airy function 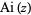 . This has the closed-form representation
. This has the closed-form representation
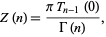 |
(2) |
where 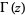 is the gamma function,
is the gamma function,
![T_n(z)=C^((n))(z)A+(d^(n-1))/(dz^(n-1))[Ai(z)Bi(z)]
-sum_(j=1)^n(n; j)C^((n-j))(z)(d^(j-1))/(dz^(j-1))[Ai(z)]^2,](http://mathworld.wolfram.com/images/equations/AiryZetaFunction/NumberedEquation3.gif) |
(3) |
where
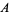 |
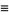 |
![int_0^infty[Ai(z)]^2dz](http://mathworld.wolfram.com/images/equations/AiryZetaFunction/Inline7.gif) |
(4) |
 |
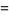 |
![1/(3^(2/3)[Gamma(1/3)]^2)](http://mathworld.wolfram.com/images/equations/AiryZetaFunction/Inline10.gif) |
(5) |
and
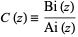 |
(6) |
(Crandall 1996; Borwein et al. 2004, p. 61).
Surprisingly, defining
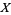 |
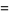 |
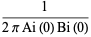 |
(7) |
 |
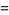 |
![(3^(5/6))/(2pi)[Gamma(2/3)]^2](http://mathworld.wolfram.com/images/equations/AiryZetaFunction/Inline16.gif) |
(8) |
 |
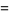 |
![(2pi)/(3^(1/6)[Gamma(1/3)]^2)](http://mathworld.wolfram.com/images/equations/AiryZetaFunction/Inline19.gif) |
(9) |
gives 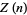 as a polynomial in
as a polynomial in 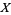 (Borwein et al. 2004, pp. 61-62). The first few such polynomials are
(Borwein et al. 2004, pp. 61-62). The first few such polynomials are
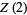 |
 |
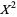 |
(10) |
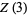 |
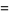 |
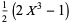 |
(11) |
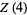 |
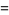 |
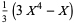 |
(12) |
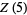 |
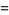 |
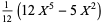 |
(13) |
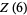 |
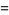 |
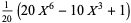 |
(14) |
(OEIS A096631 and A096632). The corresponding numerical values are approximately 0.531457, 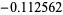 , 0.0394431,
, 0.0394431,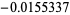 , and 0.00638927, ....
, and 0.00638927, ....
REFERENCES:
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 61-62, 2004.
Crandall, R. E. "On the Quantum Zeta Function." J. Phys. A: Math. General 29, 6795-6816, 1996.
Sloane, N. J. A. Sequences A096631 and A096632 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|