


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-7-2019
Date: 15-6-2019
Date: 19-7-2019
|
The problem in calculus of variations to find the minimal surface of a boundary with specified constraints (usually having no singularities on the surface). In general, there may be one, multiple, or no minimal surfaces spanning a given closed curve in space. The existence of a solution to the general case was independently proven by Douglas (1931) and Radó (1933), although their analysis could not exclude the possibility of singularities. Osserman (1970) and Gulliver (1973) showed that a minimizing solution cannot have singularities.
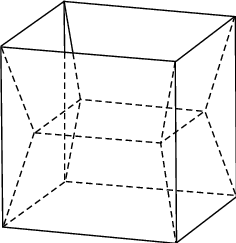
The problem is named for the Belgian physicist who solved some special cases experimentally using soap films and wire frames (Isenberg 1992, Wells 1991). The illustration above shows the 13-polygon surface obtained for a cubical wire frame.
REFERENCES:
Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 48-49, 1989.
Douglas, J. "Solution of the Problem of Plateau." Trans. Amer. Math. Soc. 33, 263-321, 1931.
Gulliver, R. "Regularity of Minimizing Surfaces of Prescribed Mean Curvature." Ann. Math. 97, 275-305, 1973.
Isenberg, C. The Science of Soap Films and Soap Bubbles. New York: Dover, 1992.
Osserman, R. "A Proof of the Regularity Everywhere of the Classical Solution to Plateau's Problem." Ann. Math. 91, 550-569, 1970.
Osserman, R. "Plateau's Problem." §1, Appendix in A Survey of Minimal Surfaces. New York: Dover, pp. 143-145, 1986.
Radó, T. "On the Problem of Plateau." Ergeben. d. Math. u. ihrer Grenzgebiete. Berlin: Springer-Verlag, 1933.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 119-121, 1999.
Stuwe, M. Plateau's Problem and the Calculus of Variations. Princeton, NJ: Princeton University Press, 1989.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 185-187, 1991.



|
|
|
|
دون أهمية غذائية.. هذا ما تفعله المشروبات السكرية بالصحة
|
|
|
|
|
|
|
المنظمة العربية للطاقة تحذر من خطر.. وهذه الدولة تتميز بجودة نفطها
|
|
|
|
|
|
|
مركز الثقافة الأسرية يواصل تقديم دورة (البروتوكول والإتيكيت) للملاكات النسوية
|
|
|