


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-11-2018
Date: 14-10-2018
Date: 28-11-2018
|
If 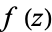 is analytic in some simply connected region
is analytic in some simply connected region 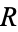 , then
, then
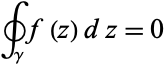 |
(1) |
for any closed contour 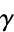 completely contained in
completely contained in 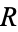 . Writing
. Writing 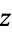 as
as
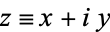 |
(2) |
and 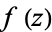 as
as
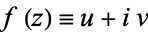 |
(3) |
then gives
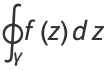 |
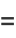 |
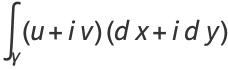 |
(4) |
 |
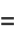 |
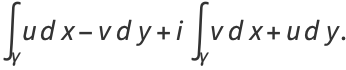 |
(5) |
From Green's theorem,
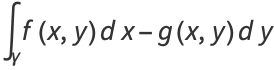 |
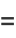 |
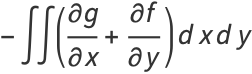 |
(6) |
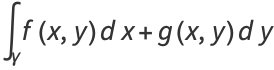 |
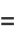 |
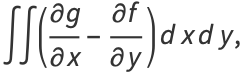 |
(7) |
so (◇) becomes
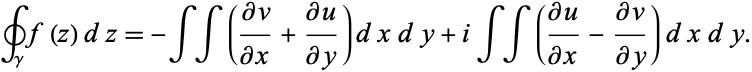 |
(8) |
But the Cauchy-Riemann equations require that
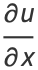 |
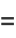 |
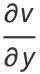 |
(9) |
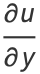 |
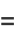 |
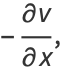 |
(10) |
so
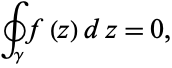 |
(11) |
Q.E.D.
For a multiply connected region,
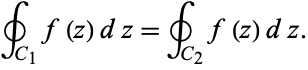 |
(12) |
REFERENCES:
Arfken, G. "Cauchy's Integral Theorem." §6.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 365-371, 1985.
Kaplan, W. "Integrals of Analytic Functions. Cauchy Integral Theorem." §9.8 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 594-598, 1991.
Knopp, K. "Cauchy's Integral Theorem." Ch. 4 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 47-60, 1996.
Krantz, S. G. "The Cauchy Integral Theorem and Formula." §2.3 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 26-29, 1999.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 363-367, 1953.
Woods, F. S. "Integral of a Complex Function." §145 in Advanced Calculus: A Course Arranged with Special Reference to the Needs of Students of Applied Mathematics. Boston, MA: Ginn, pp. 351-352, 1926.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|