

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Mittag-Leffler Function
المؤلف:
Gorenflo, R.
المصدر:
"Newtonsche Aufheizung, Abelsche Integralgleichungen zweiter Art und Mittag-Leffler-Funktionen." Z. Naturforsch
الجزء والصفحة:
...
23-11-2018
1816
Mittag-Leffler Function
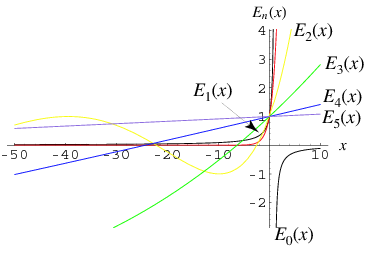
The Mittag-Leffler function (Mittag-Leffler 1903, 1905) is an entire function defined by the series
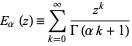 |
(1) |
for 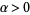 . It is related to the generalized hyperbolic functions
. It is related to the generalized hyperbolic functions 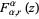 by
by
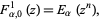 |
(2) |
and given explicitly in terms of generalized confluent hypergeometric functions as
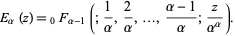 |
(3) |
It is implemented in the Wolfram Language as MittagLefflerE[a, z] and MittagLefflerE[a, b, z].
The Mittag-Leffler function arises naturally in the solution of fractional integral equations (Saxena et al. 2002), and especially in the study of the fractional generalization of the kinetic equation, random walks, Lévy flights, and so-called superdiffusive transport. The ordinary and generalized Mittag-Leffler functions interpolate between a purely exponential law and power-like behavior of phenomena governed by ordinary kinetic equations and their fractional counterparts (Lang 1999ab, Hilfer 2000, Saxena et al. 2002).
Special values for integer 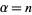 are
are
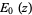 |
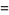 |
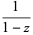 |
(4) |
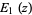 |
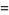 |
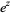 |
(5) |
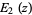 |
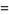 |
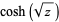 |
(6) |
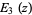 |
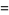 |
![1/3[e^(z^(1/3))+2e^(-z^(1/3)/2)cos(1/2sqrt(3)z^(1/3))]](http://mathworld.wolfram.com/images/equations/Mittag-LefflerFunction/Inline15.gif) |
(7) |
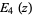 |
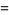 |
![1/2[cos(z^(1/4))+cosh(z^(1/4))].](http://mathworld.wolfram.com/images/equations/Mittag-LefflerFunction/Inline18.gif) |
(8) |
For half-integers 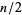 , the functions can be written explicitly as
, the functions can be written explicitly as
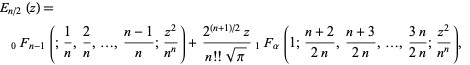 |
(9) |
giving the special value
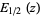 |
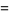 |
![e^(z^2)[1+erf(z)]](http://mathworld.wolfram.com/images/equations/Mittag-LefflerFunction/Inline22.gif) |
(10) |
 |
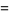 |
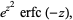 |
(11) |
for 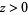 , where
, where 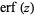 is erf and
is erf and 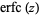 is erfc (Saxena et al. 2002). As can be seen,
is erfc (Saxena et al. 2002). As can be seen, 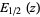 is closely related to Dawson's integral
is closely related to Dawson's integral 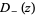 .
.
The more general Mittag-Leffler function
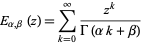 |
(12) |
can also be defined for 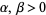 (Wiman 1905, Agarwal 1953, Humbert 1953, Humbert and Agarwal 1953, Gorenflo 1987, Miller 1993, Mainardi and Gorenflo 1996, Gorenflo 1998, Sixdeniers et al. 1999), so that
(Wiman 1905, Agarwal 1953, Humbert 1953, Humbert and Agarwal 1953, Gorenflo 1987, Miller 1993, Mainardi and Gorenflo 1996, Gorenflo 1998, Sixdeniers et al. 1999), so that
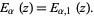 |
(13) |
The general Mittag-Leffler function can be representation in terms of Fox H-functions (Saxena et al. 2002).
The general Mittag-Leffler function satisfies
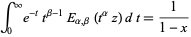 |
(14) |
for 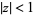 (Erdélyi et al. 1981, p. 210; Samko et al. 1993, p. 21), which gives the Laplace transform of
(Erdélyi et al. 1981, p. 210; Samko et al. 1993, p. 21), which gives the Laplace transform of 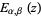 as
as
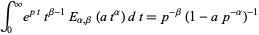 |
(15) |
for ![R[p]>|a|^(1/alpha)](http://mathworld.wolfram.com/images/equations/Mittag-LefflerFunction/Inline34.gif) and
and ![R[beta]>0](http://mathworld.wolfram.com/images/equations/Mittag-LefflerFunction/Inline35.gif) (Samko 1993, p. 21; Saxena et al. 2002).
(Samko 1993, p. 21; Saxena et al. 2002).
REFERENCES:
Agarwal, R. P. "A propos d'une note de M. Pierre Humbert." Comptes Rendus Acad. Sci. Paris 236, 2031-2032, 1953.
Dzherbashyan, M. M. Integral Transform Representations of Functions in the Complex Domain. Moscow: Nauka, 1966.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "Mittag-Leffler's Function 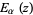 and Related Functions." §18.1 in Higher Transcendental Functions, Vol. 3. New York: Krieger, pp. 206-212, 1981.
and Related Functions." §18.1 in Higher Transcendental Functions, Vol. 3. New York: Krieger, pp. 206-212, 1981.
Gorenflo, R. "Newtonsche Aufheizung, Abelsche Integralgleichungen zweiter Art und Mittag-Leffler-Funktionen." Z. Naturforsch. A 42, 1141-1146, 1987.
Gorenflo, R.; Kilbas, A. A.; and Rogosin, S. V. "On the Generalized Mittag-Leffler Type Functions." Integral Transform. Spec. Funct. 7, 215-224, 1998.
Hilfer, R. and Anton, L. "Fractional Master Equations and Fractal Time Random Walks." Phys. Rev. E 51, R848-R851, 1995.
Hilfer, R. "On Fractional Diffusion and Its Relation with Continuous Time Random Walks." In Anomalous Diffusion: From Basics to Application: Proceedings of the XIth Max Born Symposium Held at Ladek Zdroj, Poland, 20-27 May 1998 (Ed. R. Kutner, A. Pekalski, and K. Sznaij-Weron). Berlin: Springer-Verlag, pp. 77-82, 1999.
Hilfer, R. (Ed.). Applications of Fractional Calculus in Physics. Singapore: World Scientific, 2000.
Humbert, P. "Quelques résultats relatifs à la fonction de Mittag-Leffler." Comptes Rendus Acad. Sci. Paris 236, 1467-1468, 1953.
Humbert, P. and Agarwal, R. P. "Sur la fonction de Mittag-Leffler et quelques-unes de ses généralisations." Bull. Sci. Math. Ser. 277, 180-185, 1953.
Humbert, P. and Delerue, P. "Sur une extension à deux variables de la fonction de Mittag-Leffler." Comptes Rendus Acad. Sci. Paris 237, 1059-1060, 1953.
Lang, K. R. Astrophysical Formulae, Vol. 1: Radiation, Gas Processes, and High-Energy Astrophysics, 3rd enl. rev. ed. New York: Springer-Verlag, 1999a.
Lang, K. R. Astrophysical Formulae, Vol. 2: Space, Time, Matter and Cosmology. New York: Springer-Verlag, 1999b.
Mainardi, F. and Gorenflo, R. "The Mittag-Leffler Function in the Riemann-Liouville Fractional Calculus." In Proceedings of the International Conference Dedicated to the Memory of Academician F. D. Gakhov; Held in Minsk, February 16-20, 1996 (Ed. A. A. Kilbas). Minsk, Beloruss: Beloruss. Gos. Univ., Minsk, pp. 215-225, 1996.
Meerschaert, M. M.; Benson, D. A.; Scheffler, H.-P.; and Baeumer, B. "Stochastic Solution of Space-Time Fractional Diffusion Equations." Phys. Rev. E 65, 041103, 2002.
Miller, K. S. "The Mittag-Leffler and Related Functions." Integral Transform. Spec. Funct. 1, 41-49, 1993.
Mittag-Leffler, M. G. "Sur la nouvelle fonction 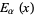 ." Comptes Rendus Acad. Sci. Paris 137, 554-558, 1903.
." Comptes Rendus Acad. Sci. Paris 137, 554-558, 1903.
Mittag-Leffler, M. G. "Sur la representation analytique d'une branche uniforme d'une fonction monogene." Acta Math. 29, 101-181, 1905.
Muldoon, M. E. and Ungar, A. A. "Beyond Sin and Cos." Math. Mag. 69, 3-14, 1996.
Podlubny, I. "The Laplace Transform Method for Linear Differential equations of the Fractional Order." 30 Oct 1997. http://arxiv.org/abs/funct-an/9710005.
Samko, S. G.; Kilbas, A. A.; and Marichev, O. I. Fractional Integrals and Derivatives. Yverdon, Switzerland: Gordon and Breach, pp. 21-22, 1993.
Saxena, R. K.; Mathai, A. M.; and Haubold, H. J. "On Fractional Kinetic Equations." 23 Jun 2002. http://arxiv.org/abs/math.CA/0206240.
Sixdeniers, J.-M.; Penson, K. A.; and Solomon, A. I. "Mittag-Leffler Coherent States." J. Phys. A: Math. Gen. 32, 7543-7563, 1999.
Sokolov, I. M.; Klafter, J. and Blumen, A. "Do Strange Kinetics Imply Unusual Thermodynamics?" Phys. Rev. E 64, 021107, 2001.
Wiman, A. "Über den Fundamentalsatz in der Theorie der Funktionen 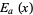 ." Acta Math. 29, 191-201, 1905.
." Acta Math. 29, 191-201, 1905.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















