

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Sine
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
"Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
25-11-2018
2775
Sine
 |
 |
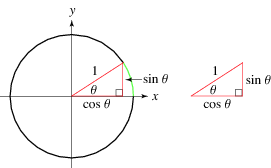
The sine function 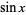 is one of the basic functions encountered in trigonometry (the others being the cosecant, cosine, cotangent, secant, and tangent). Let
is one of the basic functions encountered in trigonometry (the others being the cosecant, cosine, cotangent, secant, and tangent). Let 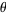 be an angle measured counterclockwise from the x-axis along an arc of the unit circle. Then
be an angle measured counterclockwise from the x-axis along an arc of the unit circle. Then 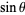 is the vertical coordinate of the arc endpoint, as illustrated in the left figure above.
is the vertical coordinate of the arc endpoint, as illustrated in the left figure above.
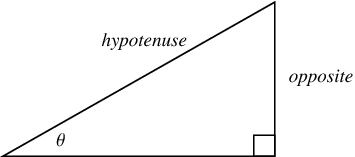
The common schoolbook definition of the sine of an angle 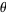 in a right triangle (which is equivalent to the definition just given) is as the ratio of the lengths of the side of the triangle opposite the angle and the hypotenuse, i.e.,
in a right triangle (which is equivalent to the definition just given) is as the ratio of the lengths of the side of the triangle opposite the angle and the hypotenuse, i.e.,
 |
(1) |
A convenient mnemonic for remembering the definition of the sine, as well as the cosine and tangent, is SOHCAHTOA (sine equals opposite over hypotenuse, cosine equals adjacent over hypotenuse, tangent equals opposite over adjacent).
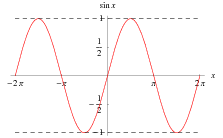
As a result of its definition, the sine function is periodic with period 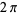 . By the Pythagorean theorem,
. By the Pythagorean theorem, 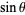 also obeys the identity
also obeys the identity
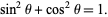 |
(2) |
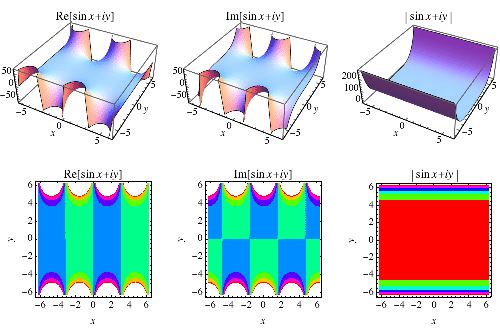 |
The definition of the sine function can be extended to complex arguments  , illustrated above, using the definition
, illustrated above, using the definition
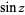 |
 |
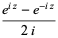 |
(3) |
 |
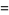 |
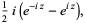 |
(4) |
where e is the base of the natural logarithm and i is the imaginary number. Sine is an entire function and is implemented in the Wolfram Language as Sin[z].
A related function known as the hyperbolic sine is similarly defined,
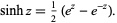 |
(5) |
The sine function can be defined analytically by the infinite sum
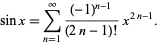 |
(6) |
It is also given by the imaginary part of the complex exponential
![sinx=I[e^(ix)].](http://mathworld.wolfram.com/images/equations/Sine/NumberedEquation5.gif) |
(7) |
The multiplicative inverse of the sine function is the cosecant, defined as
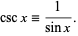 |
(8) |
The sine function is also given by the limit
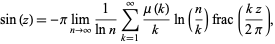 |
(9) |
where 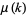 is the Möbius function and
is the Möbius function and 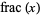 is the fractional part (M. Trott).
is the fractional part (M. Trott).
The derivative of 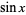 is
is
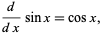 |
(10) |
and its indefinite integral is
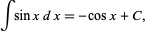 |
(11) |
where 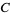 is a constant of integration.
is a constant of integration.
Using the results from the exponential sum formulas
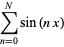 |
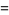 |
![I[sum_(n=0)^(N)e^(inx)]](http://mathworld.wolfram.com/images/equations/Sine/Inline20.gif) |
(12) |
 |
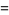 |
![I[(e^(i(N+1)x)-1)/(e^(ix)-1)]](http://mathworld.wolfram.com/images/equations/Sine/Inline23.gif) |
(13) |
 |
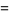 |
![I[(e^(i(N+1)x/2))/(e^(ix/2))(e^(i(N+1)x/2)-e^(-i(N+1)x/2))/(e^(ix/2)-e^(-ix/2))]](http://mathworld.wolfram.com/images/equations/Sine/Inline26.gif) |
(14) |
 |
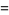 |
![(sin(1/2(N+1)x))/(sin(1/2x))I[e^(iNx/2)]](http://mathworld.wolfram.com/images/equations/Sine/Inline29.gif) |
(15) |
 |
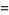 |
![(sin(1/2Nx)sin[1/2(N+1)x])/(sin(1/2x)).](http://mathworld.wolfram.com/images/equations/Sine/Inline32.gif) |
(16) |
Similarly,
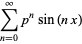 |
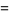 |
![I[sum_(n=0)^(infty)p^ne^(inx)]](http://mathworld.wolfram.com/images/equations/Sine/Inline35.gif) |
(17) |
 |
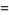 |
![I[(1-pe^(-ix))/(1-2pcosx+p^2)]](http://mathworld.wolfram.com/images/equations/Sine/Inline38.gif) |
(18) |
 |
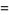 |
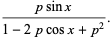 |
(19) |
The sum of 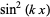 can also be done in closed form,
can also be done in closed form,
|
(20) |
A related sum identity is given by
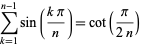 |
(21) |
(T. Drane, pers. comm., Apr. 19, 2006).
Product identities include
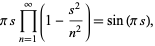 |
(22) |
which is more commonly written as an identity for the sinc function or in the form
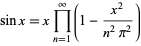 |
(23) |
(Edwards 2001, pp. 18 and 47; Borwein et al. 2004, p. 5). Another product formula is
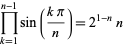 |
(24) |
(T. Drane, pers. comm., Apr. 19, 2006).
The sine function obeys the identity
![sin(ntheta)=2costhetasin[(n-1)theta]-sin[(n-2)theta]](http://mathworld.wolfram.com/images/equations/Sine/NumberedEquation15.gif) |
(25) |
and the multiple-angle formula
![sin(nx)=sum_(k=0)^n(n; k)cos^kxsin^(n-k)xsin[1/2(n-k)pi],](http://mathworld.wolfram.com/images/equations/Sine/NumberedEquation16.gif) |
(26) |
where 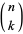 is a binomial coefficient. It is related to
is a binomial coefficient. It is related to 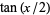 via
via
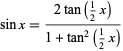 |
(27) |
(Trott 2006, p. 39).
A curious identity is given by
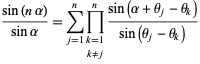 |
(28) |
for all 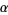 and
and 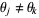 (Calogero 1999; Beylkin and Mohlenkamp 2002; Trott 2005, pp. 5-6).
(Calogero 1999; Beylkin and Mohlenkamp 2002; Trott 2005, pp. 5-6).
Cvijović and Klinowski (1995) show that the sum
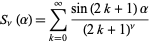 |
(29) |
has closed form for 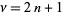 ,
,
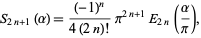 |
(30) |
where 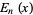 is an Euler polynomial.
is an Euler polynomial.
A continued fraction representation of 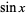 is
is
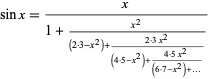 |
(31) |
(Olds 1963, p. 138).
The value of 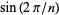 is irrational for all integers
is irrational for all integers 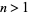 except 2, 4, and 12, for which
except 2, 4, and 12, for which 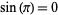 ,
, 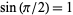 , and
, and 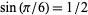 , respectively, a result that is essentially known as Niven's theorem.
, respectively, a result that is essentially known as Niven's theorem.
The Fourier transform of 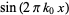 is given by
is given by
](http://mathworld.wolfram.com/images/equations/Sine/Inline56.gif) |
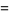 |
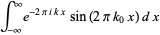 |
(32) |
 |
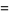 |
![1/2i[delta(k+k_0)-delta(k-k_0)].](http://mathworld.wolfram.com/images/equations/Sine/Inline61.gif) |
(33) |
A definite integral involving 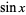 is given by
is given by
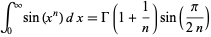 |
(34) |
for 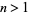 where
where 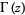 is the gamma function (R. Mabry, pers. comm., Dec. 15, 2005; T. Drane, pers. comm., Apr. 21, 2006).
is the gamma function (R. Mabry, pers. comm., Dec. 15, 2005; T. Drane, pers. comm., Apr. 21, 2006).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 71-79, 1972.
Beylkin, G. and Mohlenkamp, M. J. Proc. Nat. Acad. Sci. USA 99, 10246, 2002.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 225, 1987.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Calogero, F. "Remarkable Matrices and Trigonometric Identities. II." Commun. Appl. Math. 3, 267-270, 1999.
Cvijović, D. and Klinowski, J. "Closed-Form Summation of Some Trigonometric Series." Math. Comput. 64, 205-210, 1995.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Hansen, E. R. A Table of Series and Products. Englewood Cliffs, NJ: Prentice-Hall, 1975.
Olds, C. D. Continued Fractions. New York: Random House, 1963.
Project Mathematics. "Sines and Cosines, Parts I-III." Videotape. http://www.projectmathematics.com/sincos1.htm.
Jeffrey, A. "Trigonometric Identities." §2.4 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 111-117, 2000.
Spanier, J. and Oldham, K. B. "The Sine 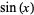 and Cosine
and Cosine 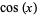 Functions." Ch. 32 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 295-310, 1987.
Functions." Ch. 32 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 295-310, 1987.
Tropfke, J. Teil IB, §1. "Die Begriffe des Sinus und Kosinus eines Winkels." In Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter, fünfter Band, zweite aufl. Berlin and Leipzig, Germany: de Gruyter, pp. 11-23, 1923.
Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.
Zwillinger, D. (Ed.). "Trigonometric or Circular Functions." §6.1 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 452-460, 1995.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















