

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Riemann Hypothesis
المؤلف:
Balazard, M. and Saias, E
المصدر:
The Nyman-Beurling Equivalent Form for the Riemann Hypothesis." Expos. Math. 18
الجزء والصفحة:
...
16-12-2018
2420
Riemann Hypothesis
First published in Riemann's groundbreaking 1859 paper (Riemann 1859), the Riemann hypothesis is a deep mathematical conjecture which states that the nontrivial Riemann zeta function zeros, i.e., the values of 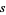 other than
other than 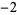 ,
, 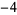 ,
, 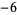 , ... such that
, ... such that 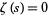 (where
(where 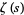 is the Riemann zeta function) all lie on the "critical line"
is the Riemann zeta function) all lie on the "critical line" ![sigma=R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline7.gif) (where
(where ![R[s]](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline8.gif) denotes the real part of
denotes the real part of  ).
).
A more general statement known as the generalized Riemann hypothesis conjectures that neither the Riemann zeta function nor any Dirichlet L-series has a zero with real part larger than 1/2.
Legend holds that the copy of Riemann's collected works found in Hurwitz's library after his death would automatically fall open to the page on which the Riemann hypothesis was stated (Edwards 2001, p. ix).
While it was long believed that Riemann's hypothesis was the result of deep intuition on the part of Riemann, an examination of his papers by C. L. Siegel showed that Riemann had made detailed numerical calculations of small zeros of the Riemann zeta function  to several decimal digits (Granville 2002; Borwein and Bailey 2003, p. 68).
to several decimal digits (Granville 2002; Borwein and Bailey 2003, p. 68).
The Riemann hypothesis has thus far resisted all attempts to prove it. Stieltjes (1885) published a note claiming to have proved the Mertens conjecture with  , a result stronger than the Riemann hypothesis and from which it would have followed. However, the proof itself was never published, nor was it found in Stieltjes papers following his death (Derbyshire 2004, pp. 160-161 and 250). Furthermore, the Mertens conjecture has been proven false, completely invalidating this claim. In the late 1940s, H. Rademacher's erroneous proof of the falsehood of Riemann's hypothesis was reported in Time magazine, even after a flaw in the proof had been unearthed by Siegel (Borwein and Bailey 2003, p. 97; Conrey 2003). de Branges has written a number of papers discussing a potential approach to the generalized Riemann hypothesis (de Branges 1986, 1992, 1994) and in fact claiming to prove the generalized Riemann hypothesis (de Branges 2003, 2004; Boutin 2004), but no actual proofs seem to be present in these papers. Furthermore, Conrey and Li (1998) prove a counterexample to de Branges's approach, which essentially means that theory developed by de Branges is not viable.
, a result stronger than the Riemann hypothesis and from which it would have followed. However, the proof itself was never published, nor was it found in Stieltjes papers following his death (Derbyshire 2004, pp. 160-161 and 250). Furthermore, the Mertens conjecture has been proven false, completely invalidating this claim. In the late 1940s, H. Rademacher's erroneous proof of the falsehood of Riemann's hypothesis was reported in Time magazine, even after a flaw in the proof had been unearthed by Siegel (Borwein and Bailey 2003, p. 97; Conrey 2003). de Branges has written a number of papers discussing a potential approach to the generalized Riemann hypothesis (de Branges 1986, 1992, 1994) and in fact claiming to prove the generalized Riemann hypothesis (de Branges 2003, 2004; Boutin 2004), but no actual proofs seem to be present in these papers. Furthermore, Conrey and Li (1998) prove a counterexample to de Branges's approach, which essentially means that theory developed by de Branges is not viable.
Proof of the Riemann hypothesis is number 8 of Hilbert's problems and number 1 of Smale's problems.
In 2000, the Clay Mathematics Institute (http://www.claymath.org/) offered a $1 million prize (http://www.claymath.org/millennium/Rules_etc/) for proof of the Riemann hypothesis. Interestingly, disproof of the Riemann hypothesis (e.g., by using a computer to actually find a zero off the critical line), does not earn the $1 million award.
The Riemann hypothesis was computationally tested and found to be true for the first  zeros by Brent et al. (1982), covering zeros
zeros by Brent et al. (1982), covering zeros  in the region
in the region  ). S. Wedeniwski used ZetaGrid (http://www.zetagrid.net/) to prove that the first trillion (
). S. Wedeniwski used ZetaGrid (http://www.zetagrid.net/) to prove that the first trillion ( ) nontrivial zeros lie on the critical line. Gourdon (2004) then used a faster method by Odlyzko and Schönhage to verify that the first ten trillion (
) nontrivial zeros lie on the critical line. Gourdon (2004) then used a faster method by Odlyzko and Schönhage to verify that the first ten trillion ( ) nontrivial zeros of the
) nontrivial zeros of the  function lie on the critical line. This computation verifies that the Riemann hypothesis is true at least for all
function lie on the critical line. This computation verifies that the Riemann hypothesis is true at least for all  less than 2.4 trillion. These results are summarized in the following table, where
less than 2.4 trillion. These results are summarized in the following table, where  indicates a gram point.
indicates a gram point.
 |
 |
source |
 |
 |
Brent et al. (1982) |
 |
 |
Wedeniwski/ZetaGrid |
 |
 |
Gourdon (2004) |
The Riemann hypothesis is equivalent to the statement that all the zeros of the Dirichlet eta function (a.k.a. the alternating zeta function)
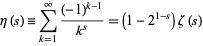 |
(1) |
falling in the critical strip ![0<R[s]<1](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline28.gif) lie on the critical line
lie on the critical line ![R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline29.gif) .
.
Wiener showed that the prime number theorem is literally equivalent to the assertion that the Riemann zeta function  has no zeros on
has no zeros on  (Hardy 1999, pp. 34 and 58-60; Havil 2003, p. 195).
(Hardy 1999, pp. 34 and 58-60; Havil 2003, p. 195).
In 1914, Hardy proved that an infinite number of values for  can be found for which
can be found for which  and
and ![R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline34.gif) (Havil 2003, p. 213). However, it is not known if all nontrivial roots
(Havil 2003, p. 213). However, it is not known if all nontrivial roots  satisfy
satisfy ![R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline36.gif) . Selberg (1942) showed that a positive proportion of the nontrivial zeros lie on the critical line, and Conrey (1989) proved the fraction to be at least 40% (Havil 2003, p. 213).
. Selberg (1942) showed that a positive proportion of the nontrivial zeros lie on the critical line, and Conrey (1989) proved the fraction to be at least 40% (Havil 2003, p. 213).
André Weil proved the Riemann hypothesis to be true for field functions (Weil 1948, Eichler 1966, Ball and Coxeter 1987). In 1974, Levinson (1974ab) showed that at least 1/3 of the roots must lie on the critical line (Le Lionnais 1983), a result which has since been sharpened to 40% (Vardi 1991, p. 142). It is known that the zeros are symmetrically placed about the line ![I[s]=0](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline37.gif) . This follows from the fact that, for all complex numbers
. This follows from the fact that, for all complex numbers  ,
,
1.  and the complex conjugate
and the complex conjugate  are symmetrically placed about this line.
are symmetrically placed about this line.
2. From the definition (1), the Riemann zeta function satisfies  , so that if
, so that if  is a zero, so is
is a zero, so is  , since then
, since then  .
.
It is also known that the nontrivial zeros are symmetrically placed about the critical line ![R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline45.gif) , a result which follows from the functional equation and the symmetry about the line
, a result which follows from the functional equation and the symmetry about the line ![I[s]=0](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline46.gif) . For if
. For if  is a nontrivial zero, then
is a nontrivial zero, then  is also a zero (by the functional equation), and then
is also a zero (by the functional equation), and then  is another zero. But
is another zero. But  and
and  are symmetrically placed about the line
are symmetrically placed about the line ![R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannHypothesis/Inline52.gif) , since
, since  , and if
, and if  , then
, then  . The Riemann hypothesis is equivalent to
. The Riemann hypothesis is equivalent to  , where
, where  is the de Bruijn-Newman constant (Csordas et al. 1994). It is also equivalent to the assertion that for some constant
is the de Bruijn-Newman constant (Csordas et al. 1994). It is also equivalent to the assertion that for some constant  ,
,
 |
(2) |
where  is the logarithmic integral and
is the logarithmic integral and  is the prime counting function (Wagon 1991). Another equivalent form states that
is the prime counting function (Wagon 1991). Another equivalent form states that
|
(3) |
where
 |
(4) |
and  is the fractional part (Balazard and Saias 2000).
is the fractional part (Balazard and Saias 2000).
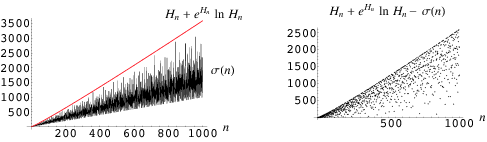
By modifying a criterion of Robin (1984), Lagarias (2000) showed that the Riemann hypothesis is equivalent to the statement that
 |
(5) |
for all  , with equality only for
, with equality only for  , where
, where  is a harmonic number and
is a harmonic number and  is the divisor function (Havil 2003, p. 207). The plots above show these two functions (left plot) and their difference (right plot) for
is the divisor function (Havil 2003, p. 207). The plots above show these two functions (left plot) and their difference (right plot) for  up to 1000.
up to 1000.
There is also a finite analog of the Riemann hypothesis concerning the location of zeros for function fields defined by equations such as
 |
(6) |
This hypothesis, developed by Weil, is analogous to the usual Riemann hypothesis. The number of solutions for the particular cases  , (3,3), (4,4), and (2,4) were known to Gauss.
, (3,3), (4,4), and (2,4) were known to Gauss.
According to Fields medalist Enrico Bombieri, "The failure of the Riemann hypothesis would create havoc in the distribution of prime numbers" (Havil 2003, p. 205).
In Ron Howard's 2001 film A Beautiful Mind, John Nash (played by Russell Crowe) is hindered in his attempts to solve the Riemann hypothesis by the medication he is taking to treat his schizophrenia.
In the Season 1 episode "Prime Suspect" (2005) of the television crime drama NUMB3RS, math genius Charlie Eppes realizes that character Ethan's daughter has been kidnapped because he is close to solving the Riemann hypothesis, which allegedly would allow the perpetrators to break essentially all internet security.
In the novel Life After Genius (Jacoby 2008), the main character Theodore "Mead" Fegley (who is only 18 and a college senior) tries to prove the Riemann Hypothesis for his senior year research project. He also uses a Cray Supercomputer to calculate several billion zeroes of the Riemann zeta function. In several dream sequences within the book, Mead has conversations with Bernhard Riemann about the problem and mathematics in general.
REFERENCES:
Balazard, M. and Saias, E. "The Nyman-Beurling Equivalent Form for the Riemann Hypothesis." Expos. Math. 18, 131-138, 2000.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 75, 1987.
Bombieri, E. "Problems of the Millennium: The Riemann Hypothesis." http://www.claymath.org/millennium/Riemann_Hypothesis/Official_Problem_Description.pdf.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 66-68, 2003.
Boutin, C. "Purdue Mathematician Claims Proof for Riemann Hypothesis." Purdue News Release. June 8, 2004. http://news.uns.purdue.edu/UNS/html4ever/2004/040608.DeBranges.Riemann.html.
Brent, R. P. "On the Zeros of the Riemann Zeta Function in the Critical Strip." Math. Comput. 33, 1361-1372, 1979.
Brent, R. P.; van de Lune, J.; te Riele, H. J. J.; and Winter, D. T. "On the Zeros of the Riemann Zeta Function in the Critical Strip. II." Math. Comput. 39, 681-688, 1982.
Caldwell, C. K. "Prime Links++." http://primes.utm.edu/links/theory/conjectures/Riemann/.
Clay Mathematics Institute. "The Riemann Hypothesis." http://www.claymath.org/millennium/Riemann_Hypothesis/.
Conrey, J. B. "At Least Two Fifths of the Zeros of the Riemann Zeta Function Are on the Critical Line." Bull. Amer. Math. Soc. 20, 79-81, 1989.
Conrey, J. B. "More than Two Fifths of the Zeros of the Riemann Zeta Function Are on the Critical Line." J. reine angew. Math.399, 1-26, 1989.
Conrey, J. B. "The Riemann Hypothesis." Not. Amer. Math. Soc. 50, 341-353, 2003. http://www.ams.org/notices/200303/fea-conrey-web.pdf.
Conrey, J. B. and Li, X.-J. "A Note on Some Positivity Conditions Related to Zeta- and  -Functions." 3 Dec 1998. http://arxiv.org/abs/math.NT/9812166.
-Functions." 3 Dec 1998. http://arxiv.org/abs/math.NT/9812166.
Csordas, G.; Smith, W.; and Varga, R. S. "Lehmer Pairs of Zeros, the de Bruijn-Newman Constant and the Riemann Hypothesis." Constr. Approx. 10, 107-129, 1994.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 371-372, 2004.
de Branges, L. "The Riemann hypothesis for Hilbert Spaces of Entire Functions." Bull. Amer. Math. Soc. 15, 1-17, 1986.
de Branges, L. "The Convergence of Euler Products." J. Func. Anal. 107, 122-210, 1992.
de Branges, L. "A Conjecture Which Implies the Riemann Hypothesis." J. Func. Anal. 121, 117-184, 1994.
de Branges, L. "Apology for the Proof of the Riemann Hypothesis." March 18, 2003. http://www.math.purdue.edu/ftp_pub/branges/apology.pdf.
de Branges, L. "Riemann Zeta Functions." May 24, 2004. http://www.math.purdue.edu/ftp_pub/branges/riemannzeta.pdf.
du Sautoy, M. The Music of the Primes: Searching to Solve the Greatest Mystery in Mathematics. New York: Harper-Collins, 2003.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Eichler, M. Introduction to the Theory of Algebraic Numbers and Functions. New York: Academic Press, 1966.
Gourdon, X. "The  First Zeros of the Riemann Zeta Function, and Zeros Computation at Very Large Height." 2004.http://numbers.computation.free.fr/Constants/Miscellaneous/zetazeros1e13-1e24.pdf.
First Zeros of the Riemann Zeta Function, and Zeros Computation at Very Large Height." 2004.http://numbers.computation.free.fr/Constants/Miscellaneous/zetazeros1e13-1e24.pdf.
Granville, A. "Prime Possibilities and Quantum Chaos." 2002. http://www.msri.org/communications/emissary/pdfs/EmissarySpring02.pdf.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Havil, J. "The Riemann Hypothesis" and "Why Is the Riemann Hypothesis Important?" §16.10 and 16.11 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 202-207, 2003.
Jacoby, M. A. Life After Genius New York: Grand Central Publishing, 2008.
Krantz, S. G. "The Riemann Hypothesis." §13.2.9 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 161, 1999.
Lagarias, J. C. "An Elementary Problem Equivalent to the Riemann Hypothesis" 22 Aug 2000. http://arxiv.org/abs/math.NT/0008177.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 25, 1983.
Levinson, N. "More than One Third of Zeros of Riemann's Zeta-Function Are on  ." Adv. Math. 13, 383-436, 1974a.
." Adv. Math. 13, 383-436, 1974a.
Levinson, N. "At Least One Third of Zeros of Riemann's Zeta-Function Are on  ." Proc. Nat. Acad. Sci. USA 71, 1013-1015, 1974b.
." Proc. Nat. Acad. Sci. USA 71, 1013-1015, 1974b.
Odlyzko, A. "The  th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors."
th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors."
Pegg, E. Jr. and Weisstein, E. W. "Seven Mathematical Tidbits." MathWorld Headline News. Nov. 8, 2004. http://mathworld.wolfram.com/news/2004-11-08/seventidbits/#3.
Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859.
Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972. Also reprinted in English translation in Edwards, H. M. Appendix. Riemann's Zeta Function. New York: Dover, pp. 299-305, 2001.
Robin, G. "Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann." J. Math. Pures Appl. 63, 187-213, 1984.
Rockmore, D. Stalking the Riemann Hypothesis: The Quest to Find the Hidden Law of Prime Numbers. New York: Vintage, 2006.
Sabbagh, K. Dr. Riemann's Zeros: The Search for the $1 Million Solution to the Greatest Problem in Mathematics. Atlantic Books, 2002.
Selberg, A. "On the Zeros of Riemann's Zeta-Function." Skr. Norske Vid.-Akad. Oslo, No. 10, 1942.
Sloane, N. J. A. Sequence A002410/M4924 in "The On-Line Encyclopedia of Integer Sequences."
Smale, S. "Mathematical Problems for the Next Century." Math. Intelligencer 20, No. 2, 7-15, 1998.
Smale, S. "Mathematical Problems for the Next Century." In Mathematics: Frontiers and Perspectives 2000 (Ed. V. Arnold, M. Atiyah, P. Lax, and B. Mazur). Providence, RI: Amer. Math. Soc., 2000.
Stieltjes, T. C. R. A. S. 1885.
te Riele, H. J. J. "Corrigendum to: On the Zeros of the Riemann Zeta Function in the Critical Strip. II." Math. Comput. 46, 771, 1986.
van de Lune, J. and te Riele, H. J. J. "On The Zeros of the Riemann Zeta-Function in the Critical Strip. III." Math. Comput. 41, 759-767, 1983.
van de Lune, J.; te Riele, H. J. J.; and Winter, D. T. "On the Zeros of the Riemann Zeta Function in the Critical Strip. IV." Math. Comput. 46, 667-681, 1986.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, 1991.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, p. 33, 1991.
Weil, A. Sur les courbes algébriques et les variétès qui s'en déduisent. Paris, 1948.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 28, 1986.
ZetaGrid Homepage. http://www.zetagrid.net/.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















