


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-12-2018
Date: 23-11-2018
Date: 16-12-2018
|
The Wiener-Hopf method is a powerful technique which enables certain linear partial differential equations subject to boundary conditions on semi-infinite domains to be solved explicitly. The method is sometimes referred to as the Wiener-Hopf technique or the Wiener-Hopf factorization.
The Wiener-Hopf method begins by applying the generalized upper and lower Fourier transforms to obtain an identity
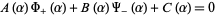 |
(1) |
on a strip
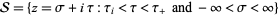 |
(2) |
of the complex 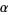 -plane where
-plane where 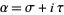 is a complex variable. Note that identity () is in terms of the unknown functions
is a complex variable. Note that identity () is in terms of the unknown functions 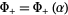 and
and 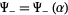 which are analytic in the half-planes
which are analytic in the half-planes 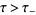 and
and 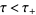 , respectively, while
, respectively, while 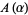 ,
, 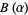 , and
, and 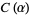 are "parameter functions" in the
are "parameter functions" in the 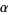 -plane which are analytic on all of
-plane which are analytic on all of 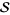 .
.
For simplicity, assume that 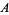 and
and 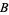 are non-zero in
are non-zero in 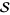 . The most fundamental step of the Wiener-Hopf process is to find a solution for
. The most fundamental step of the Wiener-Hopf process is to find a solution for 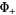 and
and 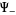 in () by finding functions
in () by finding functions 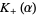 and
and 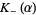 --analytic and nonzero in
--analytic and nonzero in 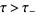 and in
and in 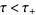 , respectively--so that
, respectively--so that
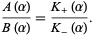 |
(3) |
Upon doing so, the factorization () can be used to rewrite () as
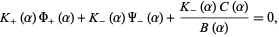 |
(4) |
whereby the last summand 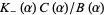 can be decomposed as
can be decomposed as
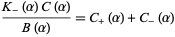 |
(5) |
for 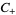 , respectively
, respectively 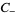 , analytic in the region of
, analytic in the region of 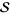 satisfying
satisfying 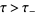 , respectively
, respectively 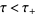 .
.
Substituting () into () and rewriting induces a function 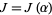 of the form
of the form
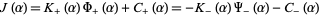 |
(6) |
which, despite being defined only in the strip 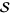 , can be defined and made analytic on the entire complex
, can be defined and made analytic on the entire complex 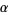 -plane by way of analytic continuation. The idea behind () is to next show the existence of positive integers
-plane by way of analytic continuation. The idea behind () is to next show the existence of positive integers 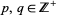 for which
for which
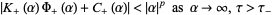 |
(7) |
and
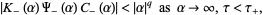 |
(8) |
whereby Liouville's theorem applies and requires that 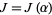 be a polynomial
be a polynomial 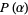 of degree less than or equal to
of degree less than or equal to 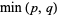 . In particular,
. In particular,
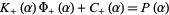 |
(9) |
and
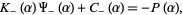 |
(10) |
thus defining 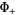 and
and 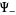 to within the arbitrary polynomial
to within the arbitrary polynomial 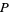 , i.e., to within a finite number of arbitrary constants which must be determined using other methods.
, i.e., to within a finite number of arbitrary constants which must be determined using other methods.
While the Wiener-Hopf method itself is a useful tool for solving various types of partial differential equations, one of its most significant strengths is the vast array of other equation solving methods derived therefrom. Indeed, the techniques spawned from the Wiener-Hopf factorization have proven useful in a number of very different circumstances across a diverse array of disciplines including theoretical and applied physics (Noble 1958), diffraction theory (Linton and McIver 2001), and fluid dynamics (Ho 2007).
REFERENCES:
Ho, J. "The Wiener-Hopf Method and Its Applications in Fluids." 2007. http://www.ms.unimelb.edu.au/publications/HoJuwen.pdf.
Linton, C. M. and McIver, P. Handbook of Mathematical Techniques for Wave/Structure Interactions. Boca Raton, FL: CRC Press, 2001.
Noble, B. Methods Based on the Wiener-Hopf Technique For the Solution of Partial Differential Equations. Belfast, Northern Ireland: Pergamon Press, 1958.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|