المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Integral Equation Neumann Series |
 1022
 01:40 مساءً
date: 30-12-2018 |
Author : Arfken, G 
Book or Source : "Neumann Series, Separable (Degenerate) Kernels." §16.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press 
Page and Part : pp. 879-890|
Read More
Date: 30-5-2018
747
Date: 23-12-2018
2412
Date: 30-5-2018
668
|
A Fredholm integral equation of the second kind
 |
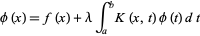(1) |
may be solved as follows. Take
 |
 |
 |
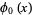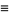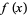(2) |
 |
 |
 |
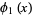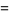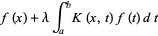(3) |
 |
 |
 |
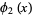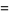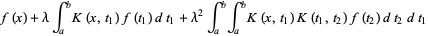(4) |
 |
 |
 |
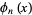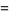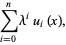(5) |
where
 |
 |
 |
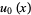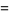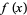(6) |
 |
 |
 |
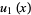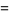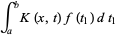(7) |
 |
 |
 |
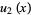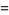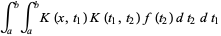(8) |
 |
 |
 |
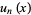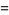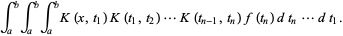(9) |
The Neumann series solution is then
 |
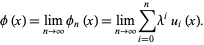(10) |
REFERENCES:
Arfken, G. "Neumann Series, Separable (Degenerate) Kernels." §16.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 879-890, 1985.
|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
