


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-3-2017
Date: 12-3-2017
Date: 4-3-2019
|
A Laurent polynomial with coefficients in the field 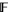 is an algebraic object that is typically expressed in the form
is an algebraic object that is typically expressed in the form
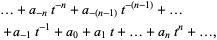 |
where the 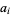 are elements of
are elements of 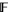 , and only finitely many of the
, and only finitely many of the 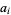 are nonzero. A Laurent polynomial is an algebraic object in the sense that it is treated as a polynomial except that the indeterminant "
are nonzero. A Laurent polynomial is an algebraic object in the sense that it is treated as a polynomial except that the indeterminant "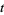 " can also have negative powers.
" can also have negative powers.
Expressed more precisely, the collection of Laurent polynomials with coefficients in a field 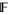 form a ring, denoted
form a ring, denoted ![F[t,t^(-1)]](http://mathworld.wolfram.com/images/equations/LaurentPolynomial/Inline7.gif) , with ring operations given by componentwise addition and multiplication according to the relation
, with ring operations given by componentwise addition and multiplication according to the relation
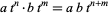 |
for all 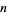 and
and 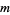 in the integers. Formally, this is equivalent to saying that
in the integers. Formally, this is equivalent to saying that ![F[t,t^(-1)]](http://mathworld.wolfram.com/images/equations/LaurentPolynomial/Inline10.gif) is the group ring of the integers and the field
is the group ring of the integers and the field 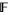 . This corresponds to
. This corresponds to ![F[t]](http://mathworld.wolfram.com/images/equations/LaurentPolynomial/Inline12.gif) (the polynomial ring in one variable for
(the polynomial ring in one variable for 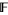 ) being the group ring or monoid ring for the monoid of natural numbers and the field
) being the group ring or monoid ring for the monoid of natural numbers and the field 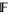 .
.
REFERENCES:
Lang, S. Undergraduate Algebra, 2nd ed. New York: Springer-Verlag, 1990.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
الطلبة المشاركون: مسابقة فنِّ الخطابة تمثل فرصة للتنافس الإبداعي وتنمية المهارات
|
|
|