المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Debye,s Asymptotic Representation |
 1512
 02:24 مساءً
date: 24-3-2019 |
Author : Itô, K. (Ed.) 
Book or Source : Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 4. Cambridge, MA: MIT Press 
Page and Part : p. 1805|
Read More
Date: 30-7-2019
1735
Date: 16-8-2018
1739
Date: 19-8-2019
1374
|
Debye's asymptotic representation is an asymptotic expansion for a Hankel function of the first kind with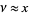 
. For
, 
, 
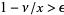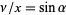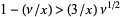, and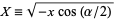 
,
![H_nu^((1))(x)∼1/(sqrt(pi))exp{ix[cosalpha+(alpha-1/2pi)sinalpha]}[(e^(ipi/4))/X+(1/8+5/(24)tan^2alpha)(3e^(3pii/4))/(2X^3)+(3/(128)+(77)/(576)tan^alpha+(385)/(3456)tan^4alpha)(3·5e^(5pii/4))/(2^2X^5)+...].](http://mathworld.wolfram.com/images/equations/DebyesAsymptoticRepresentation/NumberedEquation1.gif) |
(1) |
For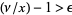 
, 
, 
, 
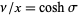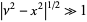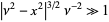, and 
,
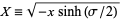![H_nu^((1))(x)∼1/(sqrt(pi))exp[x(sigmacoshsigma-sinhsigma)][1/X+(1/8-5/(24)coth^2sigma)3/(2X^3)+(3/(128)-(77)/(576)coth^2sigma+(385)/(3456)coth^4sigma)(3·5)/(2^2X^5)+...].](http://mathworld.wolfram.com/images/equations/DebyesAsymptoticRepresentation/NumberedEquation2.gif) |
(2) |
Finally, for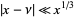 
, 
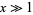, and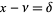 
,
![H_nu^((1))∼(6^(1/3)e^(ipi/3))/(pisqrt(3))[Gamma(1/3)x^(-1/3)-6^(1/3)e^(ipi/3)deltaGamma(2/3)x^(-2/3)+(2/5delta-delta^3)Gamma(4/3)x^(-4/3)+(3/(140)-1/4delta^2+1/4delta^4)6^(1/3)e^(ipi/3)Gamma(5/3)x^(-5/3)+...].](http://mathworld.wolfram.com/images/equations/DebyesAsymptoticRepresentation/NumberedEquation3.gif) |
(3) |
REFERENCES:
Itô, K. (Ed.). Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 4. Cambridge, MA: MIT Press, p. 1805, 1986.
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|
