


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-8-2019
Date: 29-9-2018
Date: 29-8-2019
|
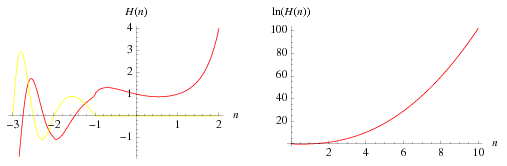
The hyperfactorial (Sloane and Plouffe 1995) is the function defined by
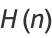 |
 |
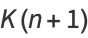 |
(1) |
 |
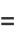 |
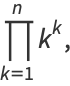 |
(2) |
where 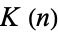 is the K-function.
is the K-function.
The hyperfactorial is implemented in the Wolfram Language as Hyperfactorial[n].
For integer values 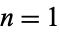 , 2, ... are 1, 4, 108, 27648, 86400000, 4031078400000, 3319766398771200000, ... (OEIS A002109).
, 2, ... are 1, 4, 108, 27648, 86400000, 4031078400000, 3319766398771200000, ... (OEIS A002109).

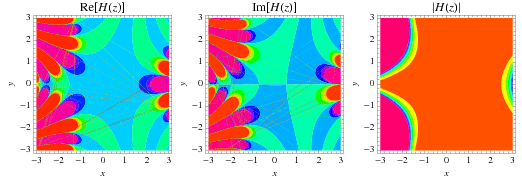
The hyperfactorial can also be generalized to complex numbers, as illustrated above.
The Barnes G-function and hyperfactorial 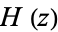 satisfy the relation
satisfy the relation
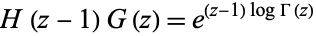 |
(3) |
for all complex 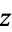 .
.
The hyperfactorial is given by the integral
![H(z)=(2pi)^(-z/2)exp[(z+1; 2)+int_0^zln(t!)dt]](http://mathworld.wolfram.com/images/equations/Hyperfactorial/NumberedEquation2.gif) |
(4) |
and the closed-form expression
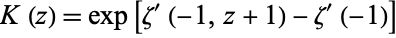 |
(5) |
for ![R[z]>0](http://mathworld.wolfram.com/images/equations/Hyperfactorial/Inline11.gif) , where
, where 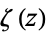 is the Riemann zeta function,
is the Riemann zeta function, 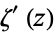 its derivative,
its derivative, 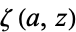 is the Hurwitz zeta function, and
is the Hurwitz zeta function, and
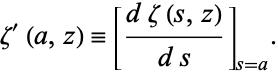 |
(6) |
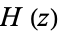 also has a Stirling-like series
also has a Stirling-like series
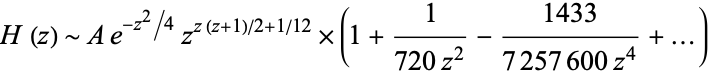 |
(7) |
(OEIS A143475 and A143476).
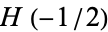 has the special value
has the special value
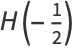 |
 |
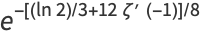 |
(8) |
 |
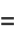 |
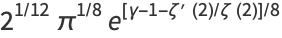 |
(9) |
 |
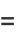 |
 |
(10) |
where 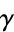 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 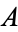 is the Glaisher-Kinkelin constant.
is the Glaisher-Kinkelin constant.
The derivative is given by
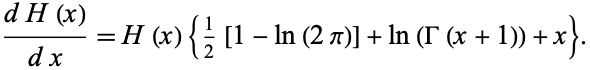 |
(11) |
REFERENCES:
Fletcher, A.; Miller, J. C. P.; Rosenhead, L.; and Comrie, L. J. An Index of Mathematical Tables, Vol. 1, 2nd ed. Reading, MA: Addison-Wesley, p. 50, 1962.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 477, 1994.
Sloane, N. J. A. Sequences A002109/M3706, A143475, and A143476 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|