
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-6-2019
Date: 1-9-2019
Date: 20-6-2019
|
Binet's first formula for 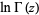 , where
, where 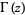 is a gamma function, is given by
is a gamma function, is given by
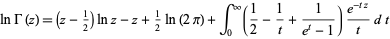 |
for ![R[z]>0](http://mathworld.wolfram.com/images/equations/BinetsLogGammaFormulas/Inline3.gif) (Erdélyi et al. 1981, p. 21; Whittaker and Watson 1990, p. 249).
(Erdélyi et al. 1981, p. 21; Whittaker and Watson 1990, p. 249).
Binet's second formula is
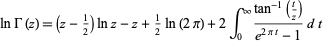 |
for ![R[z]>0](http://mathworld.wolfram.com/images/equations/BinetsLogGammaFormulas/Inline4.gif) (Erdélyi et al. 1981, p. 22; Whittaker and Watson 1990, pp. 250-251).
(Erdélyi et al. 1981, p. 22; Whittaker and Watson 1990, pp. 250-251).
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, 1981.
Whittaker, E. T. and Watson, G. N. "Binet's First Expansion for 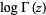 in Terms of an Infinite Integral" and "Binet's Second Expression for
in Terms of an Infinite Integral" and "Binet's Second Expression for 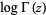 in Terms of an Infinite Integral." §12.31 and 12.32 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 248-251, 1990.
in Terms of an Infinite Integral." §12.31 and 12.32 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 248-251, 1990.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|