


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-8-2019
Date: 23-4-2019
Date: 22-5-2019
|
An algorithm for finding closed form hypergeometric identities. The algorithm treats sums whose successive terms have ratios which are rational functions. Not only does it decide conclusively whether there exists a hypergeometric sequence 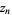 such that
such that
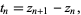 |
(1) |
but actually produces 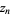 if it exists. If not, it produces
if it exists. If not, it produces 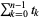 . An outline of the algorithm follows (Petkovšek et al. 1996):
. An outline of the algorithm follows (Petkovšek et al. 1996):
1. For the ratio 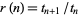 which is a rational function of
which is a rational function of 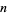 .
.
2. Write
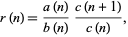 |
(2) |
where 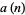 ,
, 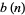 , and
, and 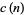 are polynomials satisfying
are polynomials satisfying
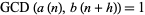 |
(3) |
for all nonnegative integers 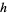 .
.
3. Find a nonzero polynomial solution 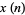 of
of
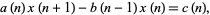 |
(4) |
if one exists.
4. Return 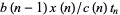 and stop.
and stop.
Petkovšek et al. (1996) describe the algorithm as "one of the landmarks in the history of computerization of the problem of closed form summation." Gosper's algorithm is vital in the operation of Zeilberger's algorithm and the machinery of Wilf-Zeilberger pairs.
REFERENCES:
Gessel, I. and Stanton, D. "Strange Evaluations of Hypergeometric Series." SIAM J. Math. Anal. 13, 295-308, 1982.
Gosper, R. W. "Decision Procedure for Indefinite Hypergeometric Summation." Proc. Nat. Acad. Sci. USA 75, 40-42, 1978.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Koepf, W. "Algorithms for 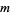 -fold Hypergeometric Summation." J. Symb. Comput. 20, 399-417, 1995.
-fold Hypergeometric Summation." J. Symb. Comput. 20, 399-417, 1995.
Koepf, W. "Gosper's Algorithm." Ch. 5 in Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 61-79, 1998.
Lafron, J. C. "Summation in Finite Terms." In Computer Algebra Symbolic and Algebraic Computation, 2nd ed. (Ed. B. Buchberger, G. E. Collins, and R. Loos). New York: Springer-Verlag, 1983.
Paule, P. and Schorn, M. "A Mathematica Version of Zeilberger's Algorithm for Proving Binomial Coefficient Identities." J. Symb. Comput. 20, 673-698, 1995.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. "Gosper's Algorithm." Ch. 5 in A=B. Wellesley, MA: A K Peters, pp. 73-99, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Pirastu, R. and Strehl, V. "Rational Summation and Gosper-Petkovšek Representation." J. Symb. Comput. 20, 617-635, 1995.
Zeilberger, D. "The Method of Creative Telescoping." J. Symb. Comput. 11, 195-204, 1991.



|
|
|
|
بـ3 خطوات بسيطة.. كيف تحقق الجسم المثالي؟
|
|
|
|
|
|
|
دماغك يكشف أسرارك..علماء يتنبأون بمفاجآتك قبل أن تشعر بها!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تواصل إقامة مجالس العزاء بذكرى شهادة الإمام الكاظم (عليه السلام)
|
|
|