


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-6-2019
Date: 2-5-2019
Date: 19-9-2019
|
Thomae's theorem, also called Thomae's transformation, is the generalized hypergeometric function identity
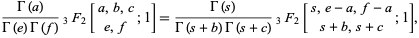 |
(1) |
where 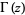 is the gamma function,
is the gamma function, 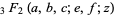 is a generalized hypergeometric function,
is a generalized hypergeometric function,
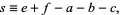 |
(2) |
and 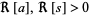 (Bailey 1935, p. 14). It is a generalization of Dixon's theorem (Slater 1966, p. 52).
(Bailey 1935, p. 14). It is a generalization of Dixon's theorem (Slater 1966, p. 52).
An equivalent formulation is given by
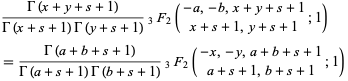 |
(3) |
(Hardy 1999, p. 104). The symmetry of this form was used by Ramanujan in his proof of the identity, which is essentially the same as Thomae's. Interestingly, this is one of the few cases in which Ramanujan gives an explicit proof of one of his propositions (Hardy 1999, p. 104).
A special case of the theorem is given by
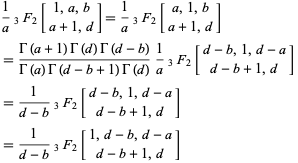 |
(4) |
(J. Sondow, pers. comm., May 25, 2003).
REFERENCES:
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: University Press, 1935.
Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge Philos. Soc. 21, 492-503, 1923.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 104-105, 1999.
Slater, L. J. Generalized Hypergeometric Functions. Cambridge, England: Cambridge University Press, p. 52, 1966.
Thomae, J. "Ueber die Funktionen welche durch Reihen von der Form dargestellt werden: 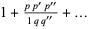 ." J. für Math. 87, 26-73, 1879.
." J. für Math. 87, 26-73, 1879.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|