


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-6-2019
Date: 12-8-2018
Date: 29-9-2019
|
Multiple series generalizations of basic hypergeometric series over the unitary groups 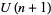 . The fundamental theorem of
. The fundamental theorem of 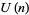 series takes
series takes 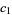 , ...,
, ..., 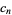 and
and 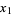 , ...,
, ..., 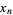 as indeterminates and
as indeterminates and 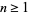 . Then
. Then
![((c_1...c_n;q)_N)/((q;q)_N)
=sum_(y_1,y_2,...,y_n>=0; |y|=N){product_(1<=r<s<=n)[(1-(x_r)/(x_s)q^(y_r-y_s))/(1-(x_r)/(x_s))]×product_(r,s=1)^n[(((x_r)/(x_s)c_s;q)_(y_r))/((q(x_r)/(x_s);q)_(y_r))][q^(y_2+2y_3+...+(n-1)y_n)]},](http://mathworld.wolfram.com/images/equations/UnBasicHypergeometricSeries/NumberedEquation1.gif) |
where it is assumed that none of the denominators vanish (Bhatnagar 1995, p. 22). The series in this theorem is called an 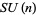 series (Milne 1985; Bhatnagar 1995, p. 22).
series (Milne 1985; Bhatnagar 1995, p. 22).
Many other 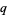 -results, including the q-binomial theorem and q-Saalschütz sum, can be generalized to
-results, including the q-binomial theorem and q-Saalschütz sum, can be generalized to 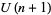 series.
series.
REFERENCES:
Bhatnagar, G. "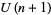 Basic Hypergeometric Series." Ch. 2 in Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University, pp. 20-38, 1995.
Basic Hypergeometric Series." Ch. 2 in Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University, pp. 20-38, 1995.
Biedenharn, L. C. and Louck, J. D. Angular Momentum in Quantum Physics: Theory and Applications. Reading, MA: Addison-Wesley, 1981.
Biedenharn, L. C. and Louck, J. D. The Racah-Wigner Algebra in Quantum Theory. Reading, MA: Addison-Wesley, 1981.
Denis, R. Y. and Gustafson, R. A. "An 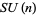
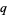 -Beta Integral Transformation and Multiple Hypergeometric Series Identities." SIAM J. Math. Anal. 23, 552-561, 1992.
-Beta Integral Transformation and Multiple Hypergeometric Series Identities." SIAM J. Math. Anal. 23, 552-561, 1992.
Gustafson, R. A. "Multilateral Summation Theorems for Ordinary and Basic Hypergeometric Series in 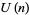 ." SIAM J. Math. Anal. 18, 1576-1596, 1987.
." SIAM J. Math. Anal. 18, 1576-1596, 1987.
Gustafson, R. A. and Krattenthaler, C. "Heine Transformations for a New Kind of Basic Hypergeometric Series in 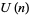 ." J. Comput. Appl. Math. 68, 151-158, 1996.
." J. Comput. Appl. Math. 68, 151-158, 1996.
Gustafson, R. A. and Krattenthaler, C. "Determinants Evaluations and 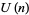 Extensions of Heine's
Extensions of Heine's 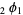 Transformations." In Special Functions, q-Series, and Related Topics (Ed. M. E. H. Ismail, D. R. Masson, and M. Rahman). Providence, RI: Amer. Math. Soc., pp. 83-89, 1997.
Transformations." In Special Functions, q-Series, and Related Topics (Ed. M. E. H. Ismail, D. R. Masson, and M. Rahman). Providence, RI: Amer. Math. Soc., pp. 83-89, 1997.
Holman, W. J. III. "Summation Theorems for Hypergeometric Series in 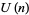 ." SIAM J. Math. Anal. 11, 523-532, 1980.
." SIAM J. Math. Anal. 11, 523-532, 1980.
Holman, W. J. III.; Biedenharn, L. C.; and Louck, J. D. "On Hypergeometric Series Well-Poised in 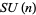 ." SIAM J. Math. Anal. 7, 529-541, 1976.
." SIAM J. Math. Anal. 7, 529-541, 1976.
Milne, S. C. "An Elementary Proof of the Macdonald Identities for 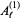 ." Adv. Math. 57, 34-70, 1985.
." Adv. Math. 57, 34-70, 1985.
Milne, S. C. "Basic Hypergeometric Series Very Well-Poised in 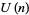 ." J. Math. Anal. Appl. 122, 223-256, 1987.
." J. Math. Anal. Appl. 122, 223-256, 1987.
Milne, S. C. "Balanced 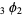 Summation for
Summation for 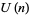 Basic Hypergeometric Series." Adv. Math. 131, 93-187, 1997.
Basic Hypergeometric Series." Adv. Math. 131, 93-187, 1997.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|