
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2018
Date: 25-4-2019
Date: 29-6-2019
|
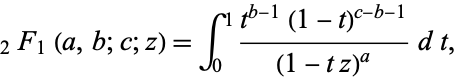 |
(1) |
where 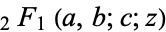 is a hypergeometric function. The solution can be written using the Euler's transformations
is a hypergeometric function. The solution can be written using the Euler's transformations
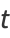 |
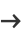 |
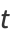 |
(2) |
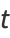 |
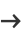 |
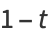 |
(3) |
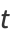 |
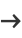 |
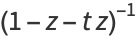 |
(4) |
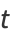 |
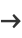 |
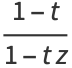 |
(5) |
in the equivalent forms
 |
 |
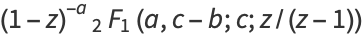 |
(6) |
 |
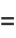 |
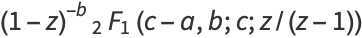 |
(7) |
 |
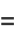 |
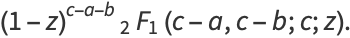 |
(8) |
Equation (7) gives Euler's convergence improvement transform of the series 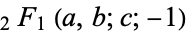 (Abramowitz and Stegun 1972, p. 555).
(Abramowitz and Stegun 1972, p. 555).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
Euler, L. Nova Acta Acad. Petropol. 7, p. 58, 1778.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 585-591, 1953.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
الأمانة العامة للعتبة الكاظمية المقدسة تستضيف مؤتمر أبناء الإمام الرضا الدولي الرابع
|
|
|