


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-4-2019
Date: 25-5-2019
Date: 22-7-2019
|
A method for finding recurrence relations for hypergeometric polynomials directly from the series expansions of the polynomials. The method is effective and easily implemented, but usually slower than Zeilberger's algorithm. Given a sum 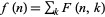 , the method operates by finding a recurrence of the form
, the method operates by finding a recurrence of the form
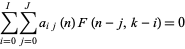 |
by proceeding as follows (Petkovšek et al. 1996, p. 59):
1. Fix trial values of 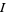 and
and 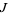 .
.
2. Assume a recurrence formula of the above form where 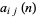 are to be solved for.
are to be solved for.
3. Divide each term of the assumed recurrence by 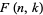 and reduce every ratio
and reduce every ratio 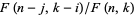 by simplifying the ratios of its constituent factorials so that only rational functions in
by simplifying the ratios of its constituent factorials so that only rational functions in 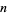 and
and 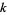 remain.
remain.
4. Put the resulting expression over a common denominator, then collect the numerator as a polynomial in 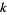 .
.
5. Solve the system of linear equations that results after setting the coefficients of each power of 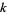 in the numerator to 0 for the unknown coefficients
in the numerator to 0 for the unknown coefficients 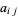 .
.
6. If no solution results, start again with larger 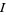 or
or 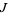 .
.
Under suitable hypotheses, a "fundamental theorem" (Verbaten 1974, Wilf and Zeilberger 1992, Petkovšek et al. 1996) guarantees that this algorithm always succeeds for large enough 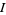 and
and 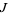 (which can be estimated in advance). The theorem also generalizes to multivariate sums and to
(which can be estimated in advance). The theorem also generalizes to multivariate sums and to 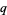 - and multi-
- and multi-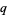 -sums (Wilf and Zeilberger 1992, Petkovšek et al. 1996).
-sums (Wilf and Zeilberger 1992, Petkovšek et al. 1996).
REFERENCES:
Fasenmyer, Sister M. C. Some Generalized Hypergeometric Polynomials. Ph.D. thesis. University of Michigan, Nov. 1945.
Fasenmyer, Sister M. C. "Some Generalized Hypergeometric Polynomials." Bull. Amer. Math. Soc. 53, 806-812, 1947.
Fasenmyer, Sister M. C. "A Note on Pure Recurrence Relations." Amer. Math. Monthly 56, 14-17, 1949.
Koepf, W. "Holonomic Recurrence Equations." Ch. 4 in Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 44-60, 1998.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. "Sister Celine's Method." Ch. 4 in A=B. Wellesley, MA: A K Peters, pp. 55-72, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Rainville, E. D. Chs. 14 and 18 in Special Functions. New York: Chelsea, 1971.
Verbaten, P. "The Automatic Construction of Pure Recurrence Relations." Proc. EUROSAM '74, ACM-SIGSAM Bull. 8, 96-98, 1974.
Wilf, H. S. and Zeilberger, D. "An Algorithmic Proof Theory for Hypergeometric (Ordinary and "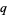 ") Multisum/Integral Identities." Invent. Math. 108, 575-633, 1992.
") Multisum/Integral Identities." Invent. Math. 108, 575-633, 1992.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|