


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-10-2019
Date: 30-3-2019
Date: 3-6-2019
|
The Andrews-Gordon identity (Andrews 1974) is the analytic counterpart of Gordon's combinatorial generalization of the Rogers-Ramanujan identities (Gordon 1961). It has a number of important applications in mathematical physics (Fulman 1999).
The identity states
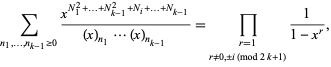 |
where 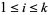 ,
, 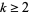 ,
,  is complex with
is complex with 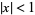 , and
, and 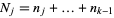 (Andrews 1974; Andrews 1984, p. 111; Fulman 1999).
(Andrews 1974; Andrews 1984, p. 111; Fulman 1999).
There are also a more general combinatorial theorems which include the Andrews-Gordon identity, Andrews's analytic generalization of the Göllnitz-Gordon identities, Gordon's partition theorem, and Schur's partition theorem as special cases. However, the statements of these theorems are quite complicated.
REFERENCES:
Andrews, G. E. "A Generalization of the Classical Partition Theorems." Trans. Amer. Math. Soc. 145, 205-221, 1969.
Andrews, G. E. On the General Rogers-Ramanujan Theorem. Providence, RI: Amer. Math. Soc., 1974.
Andrews, G. E. Encyclopedia of Mathematics and Its Applications, Vol. 2: The Theory of Partitions. Cambridge, England: Cambridge University Press, 1984.
Fulman, J. "The Rogers-Ramanujan Identities, The Finite General Linear Groups, and the Hall-Littlewood Polynomials." Proc. Amer. Math. Soc. 128, 17-25, 1999.
Gordon, B. "A Combinatorial Generalization of the Rogers-Ramanujan Identities." Amer. J. Math. 83, 393-399, 1961.
Mc Laughlin, J.; Sills, A. V.; and Zimmer, P. "Dynamic Survey DS15: Rogers-Ramanujan-Slater Type Identities." Electronic J. Combinatorics, DS15, 1-59, May 31, 2008. http://www.combinatorics.org/Surveys/ds15.pdf.



|
|
|
|
لشعر لامع وكثيف وصحي.. وصفة تكشف "سرا آسيويا" قديما
|
|
|
|
|
|
|
كيفية الحفاظ على فرامل السيارة لضمان الأمان المثالي
|
|
|
|
|
|
|
شعبة مدارس الكفيل: مخيَّم بنات العقيدة يعزِّز القيم الدينية وينمِّي مهارات اتخاذ القرار لدى المتطوِّعات
|
|
|