المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | q-Integral |
 1547
 05:01 مساءً
date: 28-8-2019 |
Author : Andrews, G. E 
Book or Source : q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math 
Page and Part : ...|
Read More
Date: 26-6-2019
2699
Date: 20-7-2019
2013
Date: 19-9-2018
1576
|
The q-analog of integration is given by
 |
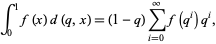(1) |
which reduces to
 |
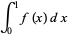(2) |
in the case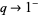 
(Andrews 1986 p. 10).
Special cases include
 |
 |
 |
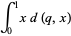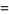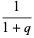(3) |
 |
 |
 |
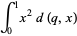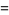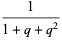(4) |
 |
 |
 |
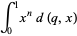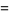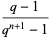(5) |
 |
 |
 |
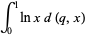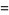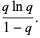(6) |
A specific case gives
![int_0^infty(x^(a-1))/(1-x)d(q,x)=([Gamma_q(1/2)]^2)/(sigma_q(a)),](http://mathworld.wolfram.com/images/equations/q-Integral/NumberedEquation3.gif) |
(7) |
where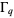 
is the q-gamma function and 
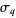is a doubly periodic sigma function. If 
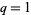, the integral reduces to
 |
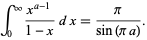(8) |
REFERENCES:
Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., 1986.
Jackson, F. H. "q-Definite Integrals." Quart. J. Math. 41, 163, 1910.
Jackson, F. H. "The q-Integral Analogous to Borel's Integral." Mess. Math. 47, 57-64, 1917.
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
ناقلا تهنئة الامين العام ...وفد الأمانة العامة للعتبة العسكرية المقدسة يزور مقرات القوات الأمنية في سامراء
|
|
|
